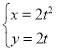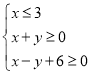题目内容
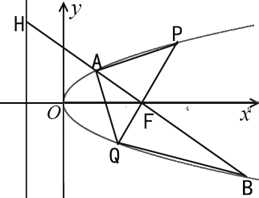
【题目】如图,![]() 是抛物线
是抛物线![]() 的焦点,过点
的焦点,过点![]() 且与坐标轴不垂直的直线交抛物线于
且与坐标轴不垂直的直线交抛物线于![]() 、
、![]() 两点,交抛物线的准线于点
两点,交抛物线的准线于点![]() ,其中
,其中![]() ,
,![]() .过点
.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() .
.
(1)求![]() 的值;
的值;
(2)求四边形![]() 的面积
的面积![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,将该直线方程与抛物线的方程联立,消去
,将该直线方程与抛物线的方程联立,消去![]() ,得到关于
,得到关于![]() 的二次方程,利用韦达定理结合
的二次方程,利用韦达定理结合![]() 可求出正数
可求出正数![]() 的值;
的值;
(2)由直线![]() 与坐标轴不垂直,所以设
与坐标轴不垂直,所以设![]() 方程为
方程为![]() ,并设点
,并设点![]() ,将直线
,将直线![]() 的方程与抛物线的方程联立,列出韦达定理,并求出
的方程与抛物线的方程联立,列出韦达定理,并求出![]() ,求出点
,求出点![]() 的坐标,可得出点
的坐标,可得出点![]() 的坐标,并可得出直线
的坐标,并可得出直线![]() 的方程,将该直线方程与抛物线的方程联立,利用韦达定理得出点
的方程,将该直线方程与抛物线的方程联立,利用韦达定理得出点![]() 的坐标,并分别计算出点
的坐标,并分别计算出点![]() 、
、![]() 到直线
到直线![]() 的距离
的距离![]() 、
、![]() ,利用三角形的面积公式可得出
,利用三角形的面积公式可得出![]() 关于
关于![]() 的表达式,设
的表达式,设![]() ,构造函数
,构造函数![]() ,利用导数求出函数
,利用导数求出函数![]() 的最小值,即可得出
的最小值,即可得出![]() 的最小值.
的最小值.
(1)设![]() 方程为
方程为![]() ,与
,与![]() 联立,消去
联立,消去![]() 整理得
整理得![]() ,
,
所以![]() ,得
,得![]() (舍去)或
(舍去)或![]() ;
;
(2)由(1)知抛物线方程为![]() ,
,![]() ,准线方程为
,准线方程为![]() .
.
因为直线![]() 与坐标轴不垂直,所以设
与坐标轴不垂直,所以设![]() 方程为
方程为![]() ,
,![]() ,
,
由![]() 得
得![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() ,
,![]() ,
,
直线![]() 的方程为
的方程为![]() ,由
,由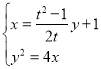 得
得![]() ,
,
所以![]() ,
,![]() ,代入
,代入![]() ,得
,得![]() ,所以
,所以![]() .
.
![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以四边形![]() 的面积
的面积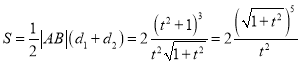 ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
所以,当![]() 时,
时,![]() 有最小值
有最小值![]() ,
,
因此,四边形![]() 的面积
的面积![]() 的最小值为
的最小值为![]() .
.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】(理)某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制各等级划分标准见下表,规定:
内,发布成绩使用等级制各等级划分标准见下表,规定:![]() 三级为合格等级,
三级为合格等级,![]() 为不合格等级.
为不合格等级.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
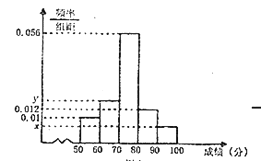
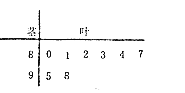
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生任选3人,求至少有1人成绩是合格等级的概率;
(3)在选取的样本中,从![]() 两个等级的学生中随机抽取了3名学生进行调研,记
两个等级的学生中随机抽取了3名学生进行调研,记![]() 表示所抽取的
表示所抽取的![]() 名学生中为
名学生中为![]() 等级的学生人数,求随机变量
等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.