题目内容
(22)P、Q、M、N四点都在椭圆x2+![]() =1上,F为椭圆在y轴正半轴上的焦点。己知
=1上,F为椭圆在y轴正半轴上的焦点。己知![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,且
共线,且![]() ·
·![]() =0。求四边形PMQN的面积的最小值和最大值。
=0。求四边形PMQN的面积的最小值和最大值。
(22)本小题主要考查椭圆和直线的方程与性质,两条直线垂直的条件,两点间的距离,不等式的性质等基本知识及综合分析能力。
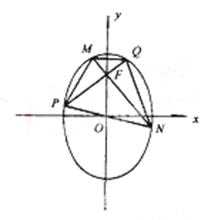
解:如图,由条件知MN和PQ是椭圆的两条弦,相交于焦点F(0,1),且PQ⊥MN,直线PQ、MN中至少有一条存在斜率,不妨设PQ的斜率为k,又PQ过点F(0,1),
故PQ方程为y=kx+1
将此式代入椭圆方程得
(2+k2)x2+2kx-1=0
设P、Q两点的坐标分别为(x1,y1),(x2,y2),则
x1=![]() ,x2=
,x2=![]()
从而 |PQ|2=(x1-x2)2+(y1-y2)2
=![]()
亦即 |PQ|=![]()
(i)当k≠0时,MN的斜率为-![]() ,同上可推得
,同上可推得
|MN|=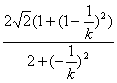
故四边形面积
S=![]() |PQ|·|MN|
|PQ|·|MN|
=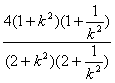
=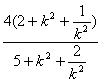
令u=k2+![]() ,得
,得
S=![]() =2(1-
=2(1-![]() )
)
因为 u= k2+![]() ≥2,
≥2,
当k=±1时,u=2,S=![]() ,
,
且S是以u为自变量的增函数,
所以![]() ≤S<2
≤S<2
(ii)当k=0时,MN为椭圆长轴,|MN|=2![]() ,|PQ|=
,|PQ|=![]() ,
,
S=![]() |PQ|·|MN|=2.
|PQ|·|MN|=2.
综合(i),(ii)知,四边形PMQN面积的最大值为2,最小值为![]() 。
。

练习册系列答案
相关题目
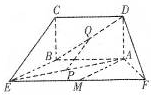 如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=
如图,五面体中,四边形ABCD是矩形,DA⊥面ABEF,且DA=1,AB∥EF,AB=