题目内容
已知椭圆C中心在坐标原点,离心率为
| ||
| 2 |
(1)求椭圆C的标准方程;
(2)过左焦点F1的直线l1,l2分别与椭圆相交于P、Q和M、N,若
| PQ |
| MN |
直线l1的斜率k(k≠0)表示四边形NQMP的面积S,求S的最小值.
分析:(1)设椭圆的方程为:
+
=1由题意可得:c=1,
=
,从而可求椭圆的方程
(II)由题意知PQ与MN垂直且相交于点F1,设PQ的方程为:y=k(x+1)
联立
消去y得(1+2k2)x2+4k2x+2k2-2=0设P(x1,y1),Q(x2,y2)则x1+x2=-
, x1x2=
,分别求出MN,PQ,代入到三角形的面积公式,结合基本不等式可求面积的最小值
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| ||
| 2 |
(II)由题意知PQ与MN垂直且相交于点F1,设PQ的方程为:y=k(x+1)
联立
|
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
解答:解:(1)设椭圆的方程为:
+
=1(a>b>0)则a2=b2+c2
由题意可得:c=1,
=
∴a=
,b=1
∴椭圆的方程为:
+y2=1
(II)由题意知PQ与MN垂直且相交于点F1,设PQ的方程为:y=k(x+1)
消去y得(1+2k2)x2+4k2x+2k2-2=0
设P(x1,y1),Q(x2,y2)则x1+x2=-
, x1x2=
∴PQ=
=
=2
•
MN=2
•
∴S△PMQ=
PQ•MN=
=2-
=2-
≥
当且仅当k2=1时取等号
∴四边形的面积S的最小值为
| x2 |
| a2 |
| y2 |
| b2 |
由题意可得:c=1,
| c |
| a |
| ||
| 2 |
| 2 |
∴椭圆的方程为:
| x2 |
| 2 |
(II)由题意知PQ与MN垂直且相交于点F1,设PQ的方程为:y=k(x+1)
|
设P(x1,y1),Q(x2,y2)则x1+x2=-
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
∴PQ=
| (1+k2)(x1-x2)2 |
| (1+k2)[(x1+x2)2-4x1x2] |
| 2 |
| 1+k2 |
| 1+2k2 |
MN=2
| 2 |
| 1+k2 |
| k2+2 |
∴S△PMQ=
| 1 |
| 2 |
| 4(1+k2)2 |
| (1+2k2)(2+k2) |
| 2k2 |
| 2k4+5k2+2 |
| 2 | ||
2k2+
|
| 16 |
| 9 |
当且仅当k2=1时取等号
∴四边形的面积S的最小值为
| 16 |
| 9 |
点评:本题主要考查了利用椭圆的性质求解椭圆的方程及直线与椭圆的位置关系的求解,解题的一般方法是联立方程,根据方程的性质进行求解,还要注意基本不等式在求解最小值中的应用.

练习册系列答案
相关题目
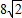 .
.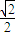 ,左焦点为F1(-1,0).
,左焦点为F1(-1,0).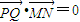 ,试用
,试用