题目内容
设函数f（x）=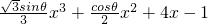
，其中θ∈[0，
]，则导数f′（-1）的取值范围是________．
（3，6]
分析：根据函数解析式求出f'（x），把x=-1代入f'（x），利用两角差的正弦公式化简，根据θ的范围和正弦函数的性质求出f'（-1）的范围．
解答：由f（x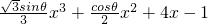）=得，f'（x）=
x2+cosθx+4，
则f′（-1）=-cosθ+4=2
+4，
∵θ∈[0，]，∴
＜θ-
＜
，∴
＜≤1，
∴-1＜2≤2，即3＜2+4≤6，
故导数f′（-1）的取值范围是（3，6]．
故答案为：（3，6]．
点评：本题考查了求函数的导数，再求导函数的函数值的范围，利用两角差的正弦公式和正弦函数的性质，进行化简并求出f'（-1）的范围．
分析：根据函数解析式求出f'（x），把x=-1代入f'（x），利用两角差的正弦公式化简，根据θ的范围和正弦函数的性质求出f'（-1）的范围．
解答：由f（x）=
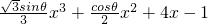得，f'（x）=x2+cosθx+4，则f′（-1）=
-cosθ+4=2+4，∵θ∈[0，
]，∴＜θ-＜，∴＜≤1，∴-1＜2
≤2，即3＜2+4≤6，故导数f′（-1）的取值范围是（3，6]．
故答案为：（3，6]．
点评：本题考查了求函数的导数，再求导函数的函数值的范围，利用两角差的正弦公式和正弦函数的性质，进行化简并求出f'（-1）的范围．
练习册系列答案
相关题目