题目内容
直线y=x+b与曲线x=
有且只有一个公共点,则实数b的取值范围是( )
| 1-y2 |
A.b=
| B.-1<b≤1或b=-
| ||||
| C.-1≤b≤1 | D.以上都不对 |
由x=
| 1-y2 |
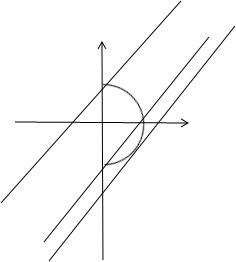
画出图象,这样因为直线与其只有一个交点,
从图上看出其三个极端情况分别是:
①直线在第四象限与曲线相切,②交曲线于(0,-1)和另一个点,③与曲线交于点(0,1).
直线在第四象限与曲线相切时解得b=-
| 2 |
当直线y=x+b经过点(0,-1)时,b=-1,所以此时-1<b≤1.
综上满足只有一个公共点的实数b 的取值范围是:-1<b≤1或b=-
| 2 |
故选B.

练习册系列答案
相关题目
若直线y=x-b与曲线
(θ∈[0,2π))有两个不同的公共点,则实数b的取值范围为( ).
|
A、(2-
| ||||
B、[2-
| ||||
C、(-∞,2-
| ||||
D、(2-
|
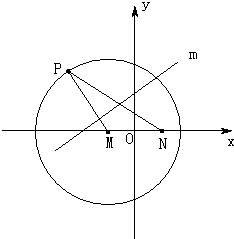 如图,已知
如图,已知