题目内容
已知函数![]() 的极小值大于零,其中
的极小值大于零,其中![]() ,
,![]() .
.
(I)求![]() 的取值范围;
的取值范围;
(II)若在![]() 的取值范围内的任意
的取值范围内的任意![]() ,函数
,函数![]() 在区间
在区间![]() 内都是增函数,
内都是增函数,
求实数![]() 的取值范围;
的取值范围;
(III)设![]() ,
,![]() ,若
,若![]() ,求证:
,求证:![]() .
.
解:(I)![]() 令
令![]() 得
得![]()
函数![]() 存在极值,
存在极值,![]() , …………(1分)
, …………(1分)
由![]() 及(I),只需考虑
及(I),只需考虑![]() 的情况.当
的情况.当![]() 变化时,
变化时,![]() 的符号及
的符号及![]() 的变化情况如下表:
的变化情况如下表:
|
|
| 0 |
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
因此,函数![]() 在
在![]() 处取得极小值
处取得极小值![]() 且
且![]()
…………(3分)
要使![]() 必有
必有![]() 可得
可得![]()
所以![]() 的取值范围是
的取值范围是![]() …………(5分)
…………(5分)
(II)由(I)知,函数![]() 在区间
在区间![]() 与
与![]() 内都是增函数.
内都是增函数.
由题设,函数![]() 在
在![]() 内是增函数,则
内是增函数,则![]() 须满足不等式组
须满足不等式组
![]() ,或
,或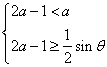 ,
,
∵![]() ∴要使不等式
∴要使不等式![]() 关于参数
关于参数![]() 恒成立,必有
恒成立,必有![]()
解得![]() 或
或![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() …………(10分)
…………(10分)
(III)用反证法证明:
假设![]() ,则
,则![]() ,或
,或![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,或
,或![]()
当![]() 时,∵函数
时,∵函数![]() 在区间
在区间![]() 内是增函数,
内是增函数,
∴![]() ,即
,即![]() 矛盾;
矛盾;
当![]() 时,∵函数
时,∵函数![]() 在区间
在区间![]() 内是增函数,
内是增函数,
∴![]() ,即
,即![]() 也矛盾;
也矛盾;
故假设不成立,即![]() 成立. …………(14分)
成立. …………(14分)

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
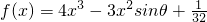 的极小值大于零,其中x∈R,θ∈[0,π].
的极小值大于零,其中x∈R,θ∈[0,π].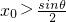 ,
,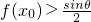 ,若f[f(x0)]=x0,求证:f(x0)=x0.
,若f[f(x0)]=x0,求证:f(x0)=x0.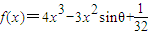 的极小值大于零,其中x∈R,θ∈[0,π].
的极小值大于零,其中x∈R,θ∈[0,π]. ,
,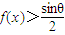 ,若f[f(x)]=x,求证:f(x)=x.
,若f[f(x)]=x,求证:f(x)=x. 的极小值大于零,其中x∈R,θ∈[0,π].
的极小值大于零,其中x∈R,θ∈[0,π].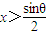 ,
, ,若f[f(x)]=x,求证:f(x)=x.
,若f[f(x)]=x,求证:f(x)=x.