题目内容
已知函数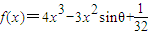 的极小值大于零,其中x∈R,θ∈[0,π].
的极小值大于零,其中x∈R,θ∈[0,π].(I)求θ的取值范围;
(II)若在θ的取值范围内的任意θ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围;
(III)设
 ,
,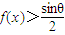 ,若f[f(x)]=x,求证:f(x)=x.
,若f[f(x)]=x,求证:f(x)=x.
【答案】分析:(I)对函数求导得,f′(x)=12x2-6xsinθ,令 ,且由题意可知x1≠x2,依据题中的条件找出函数的极小值点为
,且由题意可知x1≠x2,依据题中的条件找出函数的极小值点为 ,函数的极小值大于零?
,函数的极小值大于零?
(II)由(I)知,函数f(x)增区间(-∞,0)与 ,函数f(x)在区间(2a-1,a)内都是增函数⇒区间
,函数f(x)在区间(2a-1,a)内都是增函数⇒区间
(2a-1,a)⊆(-∞,0)或(2a-1,a)⊆( ,+∞),从而求a的取值范围
,+∞),从而求a的取值范围
(III)假设f(x)≠x则f(x)<x或f(x)>x,结合(II)函数在 的单调性进行推理,得出矛盾
的单调性进行推理,得出矛盾
解答:解:(I)f'(x)=12x2-6xsinθ令f'(x)=0得
函数f(x)存在极值,sinθ≠0,(1分)
由θ∈[0,π]及(I),只需考虑sinθ>0的情况.
当x变化时,f'(x)的符号及f(x)的变化情况如下表:
因此,函数f(x)在 处取得极小值
处取得极小值 ,且
,且 =
= (3分)
(3分)
要使 >0,必有
>0,必有 可得
可得
所以θ的取值范围是 (5分)
(5分)
(II)由(I)知,函数f(x)在区间(-∞,0)与 内都是增函数.
内都是增函数.
由题设,函数f(x)在(2a-1,a)内是增函数,则a须满足不等式组
 ,或
,或 ,
,
∵
∴要使不等式 关于参数θ恒成立,必有
关于参数θ恒成立,必有 .
.
解得a≤0或 ,所以a的取值范围是
,所以a的取值范围是 .(8分)
.(8分)
(III)用反证法证明:
假设f(x)≠x,则f(x)<x,或f(x)>x,
∵ ,
, ,
,
∴ ,或
,或
当 时,
时,
∵函数f(x)在区间 内是增函数,
内是增函数,
∴f[f(x)]<f(x),即x<f(x)矛盾;
当 时,
时,
∵函数f(x)在区间 内是增函数,
内是增函数,
∴f[f(x)]>f(x),即x>f(x)也矛盾;
故假设不成立,即f(x)=x成立.(12分)
点评:本题综合考查了利用导数的知识求解函数的极值,求函数的单调区间问题,以及结合单调性及反证法综合考查函数的综合知识.
 ,且由题意可知x1≠x2,依据题中的条件找出函数的极小值点为
,且由题意可知x1≠x2,依据题中的条件找出函数的极小值点为 ,函数的极小值大于零?
,函数的极小值大于零?
(II)由(I)知,函数f(x)增区间(-∞,0)与
 ,函数f(x)在区间(2a-1,a)内都是增函数⇒区间
,函数f(x)在区间(2a-1,a)内都是增函数⇒区间(2a-1,a)⊆(-∞,0)或(2a-1,a)⊆(
 ,+∞),从而求a的取值范围
,+∞),从而求a的取值范围(III)假设f(x)≠x则f(x)<x或f(x)>x,结合(II)函数在
 的单调性进行推理,得出矛盾
的单调性进行推理,得出矛盾解答:解:(I)f'(x)=12x2-6xsinθ令f'(x)=0得

函数f(x)存在极值,sinθ≠0,(1分)
由θ∈[0,π]及(I),只需考虑sinθ>0的情况.
当x变化时,f'(x)的符号及f(x)的变化情况如下表:

因此,函数f(x)在
 处取得极小值
处取得极小值 ,且
,且 =
= (3分)
(3分)要使
 >0,必有
>0,必有 可得
可得
所以θ的取值范围是
 (5分)
(5分)(II)由(I)知,函数f(x)在区间(-∞,0)与
 内都是增函数.
内都是增函数.由题设,函数f(x)在(2a-1,a)内是增函数,则a须满足不等式组
 ,或
,或 ,
,∵

∴要使不等式
 关于参数θ恒成立,必有
关于参数θ恒成立,必有 .
.解得a≤0或
 ,所以a的取值范围是
,所以a的取值范围是 .(8分)
.(8分)(III)用反证法证明:
假设f(x)≠x,则f(x)<x,或f(x)>x,
∵
 ,
, ,
,∴
 ,或
,或
当
 时,
时,∵函数f(x)在区间
 内是增函数,
内是增函数,∴f[f(x)]<f(x),即x<f(x)矛盾;
当
 时,
时,∵函数f(x)在区间
 内是增函数,
内是增函数,∴f[f(x)]>f(x),即x>f(x)也矛盾;
故假设不成立,即f(x)=x成立.(12分)
点评:本题综合考查了利用导数的知识求解函数的极值,求函数的单调区间问题,以及结合单调性及反证法综合考查函数的综合知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
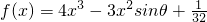 的极小值大于零,其中x∈R,θ∈[0,π].
的极小值大于零,其中x∈R,θ∈[0,π].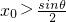 ,
,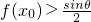 ,若f[f(x0)]=x0,求证:f(x0)=x0.
,若f[f(x0)]=x0,求证:f(x0)=x0. 的极小值大于零,其中x∈R,θ∈[0,π].
的极小值大于零,其中x∈R,θ∈[0,π].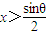 ,
, ,若f[f(x)]=x,求证:f(x)=x.
,若f[f(x)]=x,求证:f(x)=x.