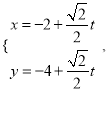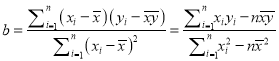题目内容
【题目】已知函数![]() ,又
,又![]() 恰为
恰为![]() 的零点.
的零点.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)当![]() 时,求证
时,求证![]()
【答案】(1)单减区间为(0,![]() ),(
),(![]() ,+∞),单增区间为(
,+∞),单增区间为(![]() );(2)见解析.
);(2)见解析.
【解析】
(1)对函数f(x)求导数,利用a的取值范围,结合导数写出f(x)的单调区间;
(2)由g(x1)=2lnx1﹣x12﹣(1-b)x1=0,g(x2)=2lnx2﹣x22﹣(1-b)x2=0,通过两式相减,整理化简可得1-b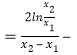 (x2+x1),再代入计算可得g′(
(x2+x1),再代入计算可得g′(![]() )
)![]() [2ln
[2ln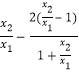 ],然后换元,构造函数,根据导数和函数的最值即可证明.
],然后换元,构造函数,根据导数和函数的最值即可证明.
(1)函数f(x)=![]() ,
,![]() ;
;
∴f′(x)=2ax+(![]() )
)![]() (x>0),
(x>0),
因为![]() ,
,![]() f′(x)=0
f′(x)=0![]() 或
或![]() ,且
,且![]() ,
,
∴当![]() 时,则f(x)的单减区间为(0,
时,则f(x)的单减区间为(0,![]() ),(
),(![]() ,+∞),单增区间为(
,+∞),单增区间为(![]() );
);
(2)当![]() 时,g(x)=2lnx-
时,g(x)=2lnx-![]() -x+bx,
-x+bx,
∴g′(x)![]() (1-b)﹣2x.
(1-b)﹣2x.
∵x1,x2(x1<x2)是g(x)的两个零点,
∴g(x1)=2lnx1﹣x12﹣(1-b)x1=0,g(x2)=2lnx2﹣x22﹣(1-b)x2=0,
两式相减可得2ln![]() (x22﹣x12)﹣(1-b)(x2﹣x1)=0,
(x22﹣x12)﹣(1-b)(x2﹣x1)=0,
∴1-b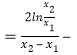 (x2+x1),
(x2+x1),
∵g′(x)![]() (1-b)﹣2x,
(1-b)﹣2x,
∴g′(![]() )
)![]() (x2+x1)﹣[
(x2+x1)﹣[ (x2+x1)]
(x2+x1)]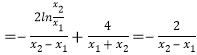 [2ln
[2ln![]() ]
]![]() [2ln
[2ln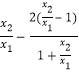 ],
],
不妨设设t=ln![]() 1,构造函数h(t)=lnt
1,构造函数h(t)=lnt![]() ,
,
则h′(t)![]() 0,
0,
∴h(t)在(1,+∞)上是增函数,
∴h(e)>h(1)=0,
∵![]() 0,
0,
∴g′(![]() )<0,又
)<0,又![]() ,
,
∴![]() .
.

【题目】已知鸡的产蛋量与鸡舍的温度有关,为了确定下一个时段鸡舍的控制温度,某企业需要了解鸡舍的温度![]() (单位:℃),对某种鸡的时段产蛋量
(单位:℃),对某种鸡的时段产蛋量![]() (单位:
(单位: ![]() )和时段投入成本
)和时段投入成本![]() (单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度
(单位:万元)的影响,为此,该企业收集了7个鸡舍的时段控制温度![]() 和产蛋量
和产蛋量![]() 的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.
的数据,对数据初步处理后得到了如图所示的散点图和表中的统计量的值.

|
|
|
|
|
|
|
17.40 | 82.30 | 3.6 | 140 | 9.7 | 2935.1 | 35.0 |
其中![]() .
.
(1)根据散点图判断, ![]() 与
与![]() 哪一个更适宜作为该种鸡的时段产蛋量
哪一个更适宜作为该种鸡的时段产蛋量![]() 关于鸡舍时段控制温度
关于鸡舍时段控制温度![]() 的回归方程类型?(给判断即可,不必说明理由)
的回归方程类型?(给判断即可,不必说明理由)
(2)若用![]() 作为回归方程模型,根据表中数据,建立
作为回归方程模型,根据表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知时段投入成本![]() 与
与![]() 的关系为
的关系为![]() ,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
,当时段控制温度为28℃时,鸡的时段产蛋量及时段投入成本的预报值分别是多少?
附:①对于一组具有有线性相关关系的数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为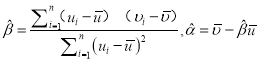
②
|
|
|
|
|
0.08 | 0.47 | 2.72 | 20.09 | 1096.63 |