Question

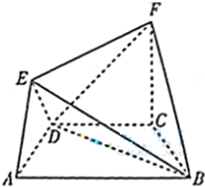（2012•山东）在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．
（Ⅰ）求证：BD⊥平面AED；
（Ⅱ）求二面角F-BD-C的余弦值．

Answer 1

分析：（Ⅰ）由题意及图可得，先由条件证得AD⊥BD及AE⊥BD，再由线面垂直的判定定理即可证得线面垂直；
（II）解法一：由（I）知，AD⊥BD，可得出AC⊥BC，结合FC⊥平面ABCD，知CA，CA，CF两两垂直，因此可以C为坐标原点，分别以CA，CB，CF所在的直线为X轴，Y轴，Z轴建立如图的空间直角坐标系，设CB=1，表示出各点的坐标，再求出两个平面的法向量的坐标，由公式求出二面角F-BD-C的余弦值即可；
解法二：取BD的中点G，连接CG，FG，由于 CB=CD，因此CG⊥BD，又FC⊥平面ABCD，BD?平面ABCD，可证明出∠FGC为二面角F-BD-C的平面角，再解三角形求出二面角F-BD-C的余弦值．

解答：（I）证明：因为四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°．所以∠ADC=∠BCD=120°．又CB=CD，
所以∠CDB=30°，因此，∠ADB=90°，AD⊥BD，
又AE⊥BD且，AE∩AD=A，AE，AD?平面AED，
所以BD⊥平面AED；
（II）解法一：由（I）知，AD⊥BD，所以AC⊥BC，
又FC⊥平面ABCD，因此CA，CB，CF两两垂直，以C为坐标原点，分别以CA，CB，CF所在的直线为X轴，Y轴，Z轴建立如图的空间直角坐标系，
不妨设CB=1，则C（0，0，0），B（0，1，0），D（

3

2

，-

1

2

，0），F（0，0，1），因此

BD

=（

3

2

，-

3

2

，0），

BF

=（0，-1，1）
设平面BDF的一个法向量为

m

=（x，y，z），则

m

•

BF

=0，

m

•

BD

=0
所以x=

3

y=

3

z，取z=1，则

m

=（

3

，1，1），
由于

CF

=（0，0，1）是平面BDC的一个法向量，
则cos＜

m

，

CF

＞=

m • CF

| CF || m |

=

1

5

=

5

5

，所以二面角F-BD-C的余弦值为

5

5

解法二：取BD的中点G，连接CG，FG，由于 CB=CD，因此CG⊥BD，又FC⊥平面ABCD，BD?平面ABCD，
所以FC⊥BD，由于FC∩CG=C，FC，CG?平面FCG．
所以BD⊥平面FCG．故BD⊥FG，所以∠FGC为二面角F-BD-C的平面角，
在等腰三角形BCD中，由于∠BCD=120°，
因此CG=

1

2

CB，又CB=CF，
所以GF=

CG2+CF2

=

5

CG，
故cos∠FGC=

5

5

，
所以二面角F-BD-C的余弦值为

5

5

点评：本题考查线面垂直的证明与二面角的余弦值的求法，解题的关键是熟练掌握线面垂直的判定定理及二面角的两种求法-向量法与几何法，本题是高中数学的典型题，也是高考中的热点题型，尤其是利用空间向量解决立体几何问题是近几年高考的必考题，学习时要好好把握向量法的解题规律．