题目内容
已知椭圆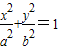
（a＞b＞0）与双曲线
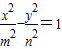（m＞0，n＞0）有相同的焦点（-c，0）和（c，0），若c是a、m的等比中项，n2是2m2与c2的等差中项，则椭圆的离心率是（ ）A．
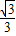
B．
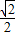
C．
D．
【答案】分析：根据是a、m的等比中项可得c2=am，根据椭圆与双曲线有相同的焦点可得a2+b2=m2+n2=c，根据n2是2m2与c2的等差中项可得2n2=2m2+c2，联立方程即可求得a和c的关系，进而求得离心率e．
解答：解：由题意：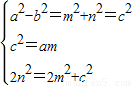
∴
，
∴
，
∴
．
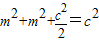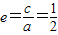故选D．
点评：本题主要考查了椭圆的性质，属基础题．
解答：解：由题意：
∴
，∴
，∴
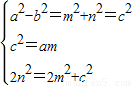
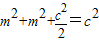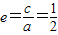．故选D．
点评：本题主要考查了椭圆的性质，属基础题．
练习册系列答案
相关题目
=1(a＞b＞0)与双曲线
=1(m＞0,n＞0)有相同的焦点(-c,0)和(c,0),若c是a、m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是( )
B.
C.
D.
=1(a＞b＞0)，F1、F2分别为椭圆的左、右焦点，A为椭圆的上的顶点，直线AF2交椭圆于另 一点B.
＝2
，
·
＝
，求椭圆的方程．
（a>b>0）,点
在椭圆上。
（a＞b＞0）的焦距为4，且与椭圆
有相同的离心率，斜率为k的直线l经过点M（0，1），与椭圆C交于不同两点A、B．
分)
（a＞b＞0）的离心率
，焦距是函数
的零点.
与椭圆交于
、
两点,
，求k的值．