题目内容
命题p：?x∈R，x2＜a，命题q：ax2+x+1＞0恒成立．若p∨q为真命题，p∧q为假命题，求a的取值范围．
解：∵命题p：?x∈R，x2＜a，命题q：ax2+x+1＞0恒成立，
∴p：a＞0，
，
∵p∨q为真命题，p∧q为假命题，
∴P真q假，或P假q真，
∴P真q假：
，
P假q真：
综上，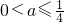
．
分析：由题设知p：a＞0，，由p∨q为真命题，p∧q为假命题，知P真q假，或P假q真，由此能求出a的取值范围．
点评：本题考查复合命题的真假判断及其应用，解题时要认真审题，仔细解答，注意合理地进行等价转化．
∴p：a＞0，
，∵p∨q为真命题，p∧q为假命题，
∴P真q假，或P假q真，
∴P真q假：
，P假q真：
综上，
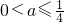．分析：由题设知p：a＞0，
，由p∨q为真命题，p∧q为假命题，知P真q假，或P假q真，由此能求出a的取值范围．点评：本题考查复合命题的真假判断及其应用，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
已知命题p：“?x∈R，|x-2|＜3”，那么?p是（ ）
| A、?x∈R，|x-2|＞3 | B、?x∈R，|x-2|≥3 | C、?x∈R，|x-2|＜3 | D、?x∈R，|x-2|≥3 |