题目内容
设等比数列 的前
的前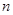 项和为
项和为 ,且
,且 ,
, ,则
,则
| A.5 | B.7 | C.9 | D.11 |
B
解析试题分析:由于等比数列 的前
的前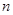 项和为
项和为 ,所以
,所以 成等比数列,所以
成等比数列,所以 .
.
考点:等比数列前n项和的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一无穷等比数列 各项的和为
各项的和为 ,第二项为
,第二项为 ,则该数列的公比为 ( )
,则该数列的公比为 ( )
A. . . | B. . . | C. . . | D. 或 或 . . |
在等比数列 中,已知前n项和
中,已知前n项和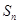 =
= ,则
,则 的值为( )
的值为( )
| A.-1 | B.1 | C.-5 | D.5 |
已知等比数列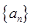 的通项公式为
的通项公式为 ,则由此数列的偶数项所组成的新数列的前
,则由此数列的偶数项所组成的新数列的前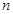 项和
项和 ( )
( )
A. | B. | C. | D. |
已知数列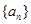 的通项
的通项 ,则
,则 ()
()
| A.0 | B. | C. | D. |
等比数列 中,
中, ,
, ,则数列
,则数列 的公比为
的公比为
A. | B. | C. | D. |
各项均为正数的等比数列 的前
的前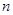 项和记为
项和记为 ( )
( )
| A.150 | B.-200 | C.150或-200 | D.-50或400 |
公比为 的等比数列
的等比数列 的各项都是正数,且
的各项都是正数,且 ,则
,则 ( )
( )
A. | B.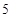 | C. | D. |
设首项为1,公比为 的等比数列{an}的前n项和为Sn,则( )
的等比数列{an}的前n项和为Sn,则( )
| A.Sn=2an-1 | B.Sn=3an-2 |
| C.Sn=4-3an | D.Sn=3-2an |