题目内容
设函数f(x)= ,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
 ,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).
,g(x)=-x2+bx,若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是 ( ).| A.x1+x2>0,y1+y2>0 |
| B.x1+x2<0,y1+y2>0 |
| C.x1+x2>0,y1+y2<0 |
| D.x1+x2<0,y1+y2<0 |
C
设F(x)=x3-bx2+1,则方程F(x)=0与f(x)=g(x)同解,
故其有且仅有两个不同零点 x1,x2.
∵F′(x)=3x2-2bx,由F′(x)=0,得x=0或x= b.
b.
易知x=0,x= b为F(x)的极值点.
b为F(x)的极值点.
又F(0)=1.
由题意F(x)的图象与x轴有两个公共点.
因此,F =0,从而b=
=0,从而b= .
.
不妨设x1<x2,则x2= b=
b= .
.
所以F(x)=(x-x1)(x- )2,比较F(x)的系数.
)2,比较F(x)的系数.
∴- x1=1,∴x1=-
x1=1,∴x1=-
 .
.
故x1+x2=
 >0,
>0,
y1+y2= =
= <0.
<0.
故其有且仅有两个不同零点 x1,x2.
∵F′(x)=3x2-2bx,由F′(x)=0,得x=0或x=
 b.
b.易知x=0,x=
 b为F(x)的极值点.
b为F(x)的极值点.又F(0)=1.
由题意F(x)的图象与x轴有两个公共点.
因此,F
 =0,从而b=
=0,从而b= .
.不妨设x1<x2,则x2=
 b=
b= .
.所以F(x)=(x-x1)(x-
 )2,比较F(x)的系数.
)2,比较F(x)的系数.∴-
 x1=1,∴x1=-
x1=1,∴x1=-
 .
.故x1+x2=

 >0,
>0,y1+y2=
 =
= <0.
<0.
练习册系列答案
相关题目
 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
 的定义域为R,且定义如下:
的定义域为R,且定义如下: (其中
(其中 是非空实数集).若非空实数集
是非空实数集).若非空实数集 满足
满足 ,则函数
,则函数 的值域为 .
的值域为 .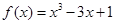 在区间
在区间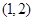 上的零点的近似值(精确度
上的零点的近似值(精确度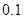 )是 .
)是 . 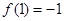





 (a>0)万元.
(a>0)万元.