题目内容
已知{an}是等差数列,a3=4,a6+a9=-10,前n项和为Sn,
(1)求通项公式an
(2)当n为何值时Sn最大,并求出最大值.
解:(1)∵{an}是等差数列,a3=4,a6+a9=-10,
∴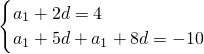 ,
,
解得a1=8,d=-2,
∴an=8+(n-d)×(-2)=-2n+10.
(2)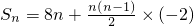
=-n2+9n
=-(n- )2
)2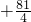 ,
,
∴当n=4或5时,Sn最大,最大值S4=S5=20.
分析:(1)由{an}是等差数列,a3=4,a6+a9=-10,利用等差数列的通项公式,列出方程组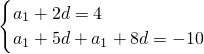 ,求出首项和公差,由此能求出an.
,求出首项和公差,由此能求出an.
(2)由a1=8,d=-2,先求出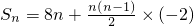 =-n2+9n,进行配方等价转化为Sn=-(n-
=-n2+9n,进行配方等价转化为Sn=-(n- )2
)2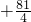 ,由此能求出当n为何值时Sn最大,并求出最大值.
,由此能求出当n为何值时Sn最大,并求出最大值.
点评:本题考查等差数列通项公式的求法和等差数列中当n为何值时Sn最大,并求出最大值.解题时要认真审题,注意配方法的合理运用.
∴
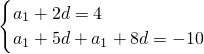 ,
,解得a1=8,d=-2,
∴an=8+(n-d)×(-2)=-2n+10.
(2)
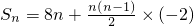
=-n2+9n
=-(n-
 )2
)2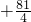 ,
,∴当n=4或5时,Sn最大,最大值S4=S5=20.
分析:(1)由{an}是等差数列,a3=4,a6+a9=-10,利用等差数列的通项公式,列出方程组
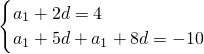 ,求出首项和公差,由此能求出an.
,求出首项和公差,由此能求出an.(2)由a1=8,d=-2,先求出
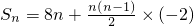 =-n2+9n,进行配方等价转化为Sn=-(n-
=-n2+9n,进行配方等价转化为Sn=-(n- )2
)2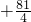 ,由此能求出当n为何值时Sn最大,并求出最大值.
,由此能求出当n为何值时Sn最大,并求出最大值.点评:本题考查等差数列通项公式的求法和等差数列中当n为何值时Sn最大,并求出最大值.解题时要认真审题,注意配方法的合理运用.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 满足:
满足: .
.