题目内容
设
分别是椭圆
的左、右焦点。
（Ⅰ）若
是该椭圆上的一个动点，求
的最大值和最小值；
（Ⅱ）是否存在过点
的直线与椭圆交于不同的两点
使得
若存在，求直线的方程；若不存在，说明理由。
解（Ⅰ）易知
设
则
当
时，即点为椭圆短轴端点时，有最小值3。
当
，即点为椭圆长轴端点时，有最大值4。
（Ⅱ）假设存在满足条件的直线，易知点
（5，0）在椭圆的外部.当直线的斜率不存在时，直线与椭圆无交点.所以直线斜率存在，设直线的方程为
由方程组
得
依题意，
得
当时，设交点
的中点为
则
又
而
不成立，综合上述，不存在直线，使得
练习册系列答案
相关题目
分别是椭圆
的左、右焦点，P是其右准线上纵坐标为
（
为半焦距）的点，且
，则椭圆的离心率是
B. 
C. 
D. 
的焦点在
轴上
的焦距为1，求椭圆
分别是椭圆的左、右焦点，
为椭圆
交
轴与点
，并且
，证明：当
变化时，点
在某定直线上。
分别是椭圆
的左、右焦点．
是该椭圆上的一点，且
，求
的面积；
是该椭圆上的一个动点，求
的最大值和最小值；
的直线
与椭圆交于不同的两点
，且
为锐角（其中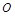
为坐标原点），求直线
的取值范围．
分别是椭圆的
左，右焦点。
是第一象限内该椭圆上的一点，且
，求点
的直线与椭圆交于不同的两点
，且
为锐角（其中O为坐标原点），求直线
的斜率
的取值范围。
分别是椭圆
的左、右焦点，过
斜率为1的直线
与
相交于
两点，且
成等差数列。
满足
，求