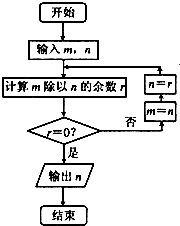
题目内容
【题目】已知椭圆C: ![]() (a>b>0 ) 经过点 P(1,
(a>b>0 ) 经过点 P(1, ![]() ),离心率 e=
),离心率 e= ![]()
(Ⅰ)求椭圆C的标准方程.
(Ⅱ)设过点E(0,﹣2 ) 的直线l 与C相交于P,Q两点,求△OPQ 面积的最大值.
【答案】解:(Ⅰ)由点 ![]() 在椭圆上得,
在椭圆上得, ![]() ①
①
又e= ![]() =
= ![]() ②,c2=a2﹣b2③
②,c2=a2﹣b2③
由①②③得c2=3,a2=4,b2=1,
故椭圆C的标准方程为 ![]() .
.
(Ⅱ)当直线l的斜率不存在,不合题意,可设直线l:y=kx﹣2,P(x1 , y1),Q(x2 , y2),
将y=kx﹣2代入椭圆方程x2+4y2=4,可得(1+4k2)x2﹣16kx+12=0,
由△=162k2﹣48(1+4k2)>0,解得k> ![]() 或k<﹣
或k<﹣ ![]() .
.
x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
|PQ|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]()
![]() =4
=4 ![]()
![]() ,
,
又O到直线PQ的距离d= ![]() ,
,
则S△OPQ= ![]() d|PQ|=4
d|PQ|=4 ![]() ,
,
设t= ![]() ,(t>0),则4k2=3+t2 ,
,(t>0),则4k2=3+t2 ,
即有S△OPQ= ![]() =
= ![]()
由t+ ![]() ≥2
≥2 ![]() =4,
=4,
当且仅当t=2,即k=± ![]() 时等号成立,足判别式大于0.
时等号成立,足判别式大于0.
则S△OPQ≤1.
故△OPQ 面积的最大值为1
【解析】(Ⅰ)运用椭圆的离心率公式和点满足椭圆方程,以及a,b,c的关系,解方程可得a,b,进而得到椭圆方程;(Ⅱ)当直线l的斜率不存在,不合题意,可设直线l:y=kx﹣2,P(x1 , y1),Q(x2 , y2),联立椭圆方程,消去y,得到x的方程,运用判别式大于0和韦达定理,以及弦长公式,点到直线的距离公式,由三角形的面积公式,运用换元法和基本不等式即可得到所求最大值.

练习册系列答案
相关题目