题目内容
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在过点![]() 的直线
的直线![]() 与
与![]() 相交于不同的两点
相交于不同的两点![]() ,满足
,满足![]() ?
?
若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由题意布列![]() 的方程组,解之即可;(2)假设存在符合题意的直线
的方程组,解之即可;(2)假设存在符合题意的直线![]() ,
,
由题意直线![]() 存在斜率,设直线
存在斜率,设直线![]() 的方程为
的方程为![]() ,由
,由 ,消去
,消去![]() 得
得![]() ,利用韦达定理表示
,利用韦达定理表示![]() ,
,
即可求出直线![]() 的方程.
的方程.
试题解析:
(Ⅰ)设椭圆![]() 的方程为
的方程为![]()
由![]() 得
得![]() ,则
,则![]()
所以![]() 的方程为
的方程为![]() 且经过点
且经过点![]()
则![]() ,解得
,解得![]()
故椭圆![]() 的方程为
的方程为![]()
(Ⅱ)假设存在符合题意的直线![]() ,
,
由题意直线![]() 存在斜率,设直线
存在斜率,设直线![]() 的方程为
的方程为![]() ,
,
由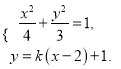 ,消去
,消去![]() 得
得![]()
由![]() 得
得![]() ,解得
,解得![]()
设![]() ,
, ![]() ,则
,则![]() ,
, ![]()
由![]() 得
得![]()
则![]()
即![]()
所以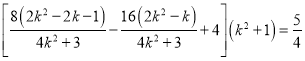
整理得![]() ,解得
,解得![]()
又![]() ,所以
,所以![]()
故存在直线![]() 满足条件,其方程为
满足条件,其方程为![]() ,即
,即![]()

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三全体![]() 名学生中随机抽取了
名学生中随机抽取了![]() 名学生的体检表,并得到如图所示的频率分布直方图.
名学生的体检表,并得到如图所示的频率分布直方图.
(Ⅰ)若直方图中后四组的频数成等差数列,计算高三全体学生视力在![]() 以下的人数,并估计这
以下的人数,并估计这![]() 名学生视力的中位数(精确到
名学生视力的中位数(精确到![]() );
);
(Ⅱ)学习小组发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对高三全体成绩名次在前![]() 名和后
名和后![]() 名的学生进行了调查,部分数据如表1,根据表1及临界表2中的数据,能否在犯错误的概率不超过
名的学生进行了调查,部分数据如表1,根据表1及临界表2中的数据,能否在犯错误的概率不超过![]() 的前提下认为视力与学习成绩有关系?
的前提下认为视力与学习成绩有关系?

年段名次 是否近视 | 前 | 后 |
近 视 |
| |
|
|
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
(参考公式:  ,其中
,其中![]() )
)