题目内容
设0＜θ＜2π，如果sinθ＞0且cos2θ＜0，那么θ的取值范围是（ ）A．
π＜θ＜
πB．
π＜θ＜2πC．π＜θ＜
πD．
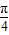
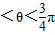
【答案】分析：由sinθ＞0，可得0＜θ＜π，再由cos2θ＜0可得1-2sin2θ＜0，进而可得sinθ＞
，或sinθ＜-
，解得θ的范围，与上面范围求交集即可．
解答：解：∵0＜θ＜2π，sinθ＞0，
∴0＜θ＜π，
又∵cos2θ＜0，∴1-2sin2θ＜0，
∴sinθ＞
，或sinθ＜-
∴
＜θ＜
，或
＜θ＜
，
结合0＜θ＜π，可得
＜θ＜
，
故选D
点评：本题考查三角函数符号问题，由二倍角公式变形整理得单角的三角函数范围是解决问题的关键，属基础题．
，或sinθ＜-，解得θ的范围，与上面范围求交集即可．解答：解：∵0＜θ＜2π，sinθ＞0，
∴0＜θ＜π，
又∵cos2θ＜0，∴1-2sin2θ＜0，
∴sinθ＞
，或sinθ＜-∴
＜θ＜，或＜θ＜，结合0＜θ＜π，可得
＜θ＜，故选D
点评：本题考查三角函数符号问题，由二倍角公式变形整理得单角的三角函数范围是解决问题的关键，属基础题．
练习册系列答案
轻松课堂单元测试AB卷系列答案
小题狂做系列答案
相关题目
(t为参数)，点P在直线上，且与点M0(-4，0)的距离为2，如果该直线的参数方程改写成
(t为参数)，则在这个方程中点P对应的t值为( )
(t为参数)，点P在直线上，且与点M0(-4，0)的距离为2，如果该直线的参数方程改写成
(t为参数)，则在这个方程中点P对应的t值为( )
