题目内容
设函数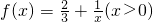 ,数列{an}满足
,数列{an}满足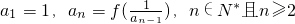 .
.
(1)求数列{an}的通项公式;
(2)对n∈N*,设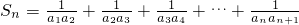 ,若
,若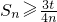 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
解:(I)由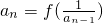 可得an-a n-1=
可得an-a n-1= ,n≥2,
,n≥2,
故数列{an}为等差数列,
又a1=1,
它的通项公式an=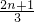 .
.
(II)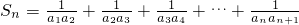 ,
,
由(I)得an=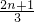 .an+1=
.an+1=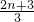 .
.
∴anan+1=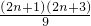 ,
,
∴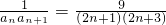 =
=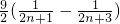 ,
,
∴Sn= =
=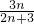 ,
,
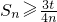 ?
? ?t
?t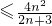 ,令g(n)=
,令g(n)= ,
,
g(n)=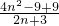 =2n+3+
=2n+3+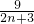 -6,由于2n+3≥5,故g(n)的最小值为
-6,由于2n+3≥5,故g(n)的最小值为 ,
,
∴t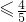 ,
,
∴实数t的取值范围(-∞, ].
].
分析:(I)由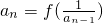 推出递推关系式an-a n-1=
推出递推关系式an-a n-1= ,n≥2,从而有数列{an}为等差数列,最后写出通项公式.
,n≥2,从而有数列{an}为等差数列,最后写出通项公式.
(II)由(I)得an=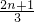 .an+1=
.an+1=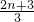 .得出anan+1=
.得出anan+1=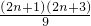 ,从而有
,从而有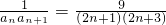 =
=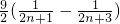 ,利用拆项法求和Sn,再结合题设利用函数的最小值,从而求得实数t的取值范围.
,利用拆项法求和Sn,再结合题设利用函数的最小值,从而求得实数t的取值范围.
点评:本题考查数列的求和、数列的综合运用,解题时要认真审题,仔细解答,注意递推公式的灵活运用.
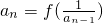 可得an-a n-1=
可得an-a n-1= ,n≥2,
,n≥2,故数列{an}为等差数列,
又a1=1,
它的通项公式an=
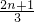 .
.(II)
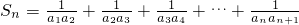 ,
,由(I)得an=
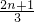 .an+1=
.an+1=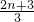 .
.∴anan+1=
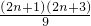 ,
,∴
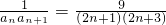 =
=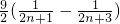 ,
,∴Sn=
 =
=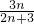 ,
,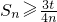 ?
? ?t
?t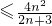 ,令g(n)=
,令g(n)= ,
,g(n)=
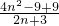 =2n+3+
=2n+3+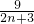 -6,由于2n+3≥5,故g(n)的最小值为
-6,由于2n+3≥5,故g(n)的最小值为 ,
,∴t
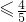 ,
,∴实数t的取值范围(-∞,
 ].
].分析:(I)由
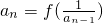 推出递推关系式an-a n-1=
推出递推关系式an-a n-1= ,n≥2,从而有数列{an}为等差数列,最后写出通项公式.
,n≥2,从而有数列{an}为等差数列,最后写出通项公式.(II)由(I)得an=
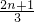 .an+1=
.an+1=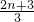 .得出anan+1=
.得出anan+1=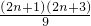 ,从而有
,从而有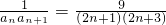 =
=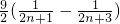 ,利用拆项法求和Sn,再结合题设利用函数的最小值,从而求得实数t的取值范围.
,利用拆项法求和Sn,再结合题设利用函数的最小值,从而求得实数t的取值范围.点评:本题考查数列的求和、数列的综合运用,解题时要认真审题,仔细解答,注意递推公式的灵活运用.

练习册系列答案
相关题目
 ,数列{an}满足
,数列{an}满足
 ,试比较 Sn与
,试比较 Sn与 的大小,并加以证明.
的大小,并加以证明. ,数列{an}满足
,数列{an}满足
 ,试比较 Sn与
,试比较 Sn与 的大小,并加以证明.
的大小,并加以证明.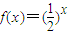 ,数列{an} 满足
,数列{an} 满足 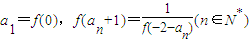
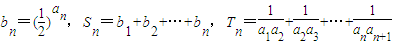 ,求 Sn与 Tn.
,求 Sn与 Tn. ,数列{an}满足
,数列{an}满足 .
. ,这些项能够构成以a1为首项,q(0<q<5,q∈N*)为公比的等比数列
,这些项能够构成以a1为首项,q(0<q<5,q∈N*)为公比的等比数列 ,k∈N*.若存在,写出nk关于k的表达式;若不存在,说明理由.
,k∈N*.若存在,写出nk关于k的表达式;若不存在,说明理由.