题目内容
设函数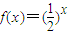
，数列{an} 满足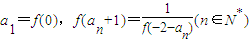 
（1）求数列{an} 的通项公式；
（2）令
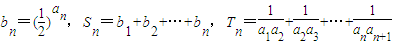，求 Sn与 Tn．
【答案】分析：（1）首先求出a1的值，然后根据
，得出
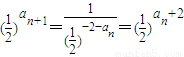，进而得出an+1-an=2，从而确定数列{an} 是首项为1，公差为2的等差数列，即可求出通项公式；
（2）首先由（1）能够得出数列{bn}是首项为
，公比为
的等比数列，然后根据等比数列的前n项和求出 Sn，再根据裂项的方法求出Tn．
解答：解：（1）∵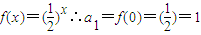
又∵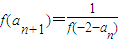
∴
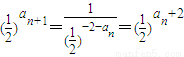
∴an+1=an+2即an+1-an=2，∴数列{an} 是首项为1，公差为2的等差数列
∴an=1+（n-1）×2=2n-1．
（2）∵
∴
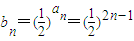
即数列{bn}是首项为
，公比为
的等比数列
Sn=b1+b2+…+bn=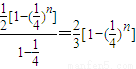
Tn=
+
+…+
=
+
+…+
=
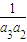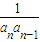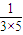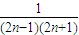[（1-
）+
]=
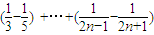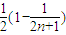（13分）
点评：本题考查了数列求和和等比数列的通项公式，对于等差数列和等比数列用公式即可求出前n项和，对于其他数列要根据数列的特点采取不同的方法求前n项和，属于中档题．
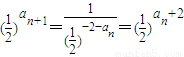，得出，进而得出an+1-an=2，从而确定数列{an} 是首项为1，公差为2的等差数列，即可求出通项公式；（2）首先由（1）能够得出数列{bn}是首项为
，公比为的等比数列，然后根据等比数列的前n项和求出 Sn，再根据裂项的方法求出Tn．解答：解：（1）∵
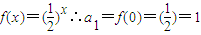
又∵
∴
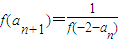
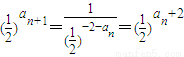
∴an+1=an+2即an+1-an=2，∴数列{an} 是首项为1，公差为2的等差数列
∴an=1+（n-1）×2=2n-1．
（2）∵
∴
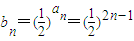
即数列{bn}是首项为
，公比为的等比数列Sn=b1+b2+…+bn=
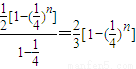
Tn=
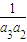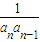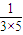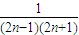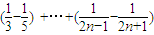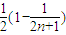++…+=++…+=[（1-）+]=（13分）点评：本题考查了数列求和和等比数列的通项公式，对于等差数列和等比数列用公式即可求出前n项和，对于其他数列要根据数列的特点采取不同的方法求前n项和，属于中档题．
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
，数列{an}满足
，试比较 Sn与
的大小，并加以证明．
，数列{an}满足
，试比较 Sn与
的大小，并加以证明．
，数列{an}满足
．
，这些项能够构成以a1为首项，q（0＜q＜5，q∈N*）为公比的等比数列
，k∈N*．若存在，写出nk关于k的表达式；若不存在，说明理由．