Question

如图，在直三棱柱ABC—A₁B₁C₁中，AC=3，BC=4，AB=5，AA₁=4，点D是AB的中点.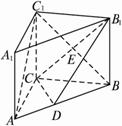

(1)求证：AC⊥BC₁；

(2)求证：AC₁∥平面CDB₁；

(3)求异面直线AC₁与B₁C所成角的余弦值.

Answer 1

解法一：(1)证明：∵直三棱柱ABC—A₁B₁C₁底面三边长AC=3，BC=4，AB=5，∴AC⊥BC，且BC₁在平面ABC内的射影为BC，∴AC⊥BC₁.?

 (2)证明：设CB₁与C₁B的交点为E，连结DE，?

∵D是AB的中点，E是BC₁的中点，?

∴DE∥AC₁.?

∵DE平面CDB₁，AC₁平面CDB₁，∴AC₁∥平面CDB₁.?

(3)∵DE∥AC₁,∴∠CED为AC₁与B₁C所成的角.?

在△CED中，ED=AC₁=,CD=AB=,CE=CB₁=2,?

∴cos∠CED=.?

∴异面直线AC₁与B₁C所成角的余弦值为.?

解法二：∵直三棱柱ABC—A₁B₁C₁底面三边长AC=3，BC=4，AB=5，?

∵AC、BC、C₁C两两垂直，如图，以C为坐标原点，直线CA、CB、CC₁分别为x轴、y轴、z轴，建立空间直角坐标系，则

C(0,0,0),A(3,0,0),C₁(0,0,4),B(0,4,0),B₁(0,4,4),D(,2,0).?

?

(1)证明：∵=(-3,0,0), =(0,-4,4),?

∴•=0.∴AC⊥BC₁.?

(2)证明：设CB₁与C₁B的交点为E，则?E(0,2,2).??

∵=(-,0,2),=(-3,0,4),?

∴.?

∴DE∥AC₁.?

∵DE平面CDB₁，AC₁平面CDB₁，∴AC₁∥平面CDB₁.?

(3)∵=(-3,0,4),=(0,4,4),?

∴cos〈,〉=.?                                                                                                                                                                                                                                                             

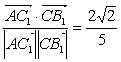∴异面直线AC₁与B₁C所成角的余弦值为.