题目内容
已知半径为2,圆心在直线 上的圆C.
上的圆C.
(Ⅰ)当圆C经过点A(2,2)且与 轴相切时,求圆C的方程;
轴相切时,求圆C的方程;
(Ⅱ)已知E(1,1),F(1,-3),若圆C上存在点Q,使 ,求圆心的横坐标
,求圆心的横坐标 的取值范围.
的取值范围.
 上的圆C.
上的圆C.(Ⅰ)当圆C经过点A(2,2)且与
 轴相切时,求圆C的方程;
轴相切时,求圆C的方程;(Ⅱ)已知E(1,1),F(1,-3),若圆C上存在点Q,使
 ,求圆心的横坐标
,求圆心的横坐标 的取值范围.
的取值范围.(Ⅰ) ;(Ⅱ)
;(Ⅱ)
 ;(Ⅱ)
;(Ⅱ)
试题分析:(Ⅰ)因为原心在直线
 上故可设原心为
上故可设原心为 ,则可根据圆心和圆上的点的距离为半径列出方程。又因为此圆与
,则可根据圆心和圆上的点的距离为半径列出方程。又因为此圆与 轴相切则
轴相切则 ,解方程组可得
,解方程组可得 。(Ⅱ)设
。(Ⅱ)设 ,根据
,根据 可得
可得 ,即点
,即点 在直线
在直线 上。又因为点
上。又因为点 在圆
在圆 上,所以直线
上,所以直线 与圆
与圆 必有交点。所以圆心到直线的距离小于等于半径。
必有交点。所以圆心到直线的距离小于等于半径。试题解析:解: (Ⅰ)∵圆心在直线
 上,
上,∴可设圆的方程为
 ,
,其圆心坐标为(
 ; 2分
; 2分∵圆经过点A(2,2)且与
 轴相切,
轴相切,∴有

解得
 ,
,∴所求方程是:
 . 5分
. 5分(Ⅱ)设
 ,由
,由 得:
得: ,解得
,解得 ,所以点
,所以点 在直线
在直线 上。
上。因为点
 在圆
在圆 :
: 上,所以圆
上,所以圆 与直线
与直线 必有交点。
必有交点。因为圆
 圆心到直线
圆心到直线 的距离
的距离 ,解得
,解得 。
。所以圆
 的横坐标
的横坐标 的取值范围是
的取值范围是 。
。
练习册系列答案
相关题目
 ,圆心在直线
,圆心在直线 :
: 上,且被直线
上,且被直线 :
: 所截弦的长为
所截弦的长为 的圆的方程.
的圆的方程. 的半径为( )
的半径为( )



 的圆
的圆 中,弦
中,弦 、
、 相交于
相交于 ,
, ,
, ,则圆心
,则圆心
 的圆
的圆 中,
中, ,
, 为
为 的中点,
的中点,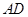 的延长线交圆
的延长线交圆 ,则线段
,则线段 的长为 .
的长为 .
 、
、 是半径为
是半径为 的圆
的圆 的两条弦,它们相交于
的两条弦,它们相交于 ,且
,且 ,
, ,则
,则 ____.
____.
 的内部,则实数m的取值范围是( )
的内部,则实数m的取值范围是( )



 是半圆
是半圆 的直径,
的直径, 在
在 与半圆相切于点
与半圆相切于点 ,
, ,若
,若 ,
, ,则
,则 .
.