Question

已知函数f（x）=x|m-x|（x∈R），且f（1）=0．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）作出函数f（x）的图象，并指出函数f（x）的单调区间；
（Ⅲ）求不等式f(x)＞

1

4

的解集．

Answer 1

分析：本题考查的是分段函数问题．在解答时，对（Ⅰ）由f（1）=0即可求得m的值，从而获得函数f（x）的解析式；对（Ⅱ）根据自变量的取值范围不同分别不同段上的函数图象即可，注意是两部分开口不同的二次函数图象，进而由图象直接读出函数的单调区间即可；对（Ⅲ）可采取通过函数解答不等式和分类讨论直接解绝对值不等式两种方法处理；
法二：对x|1-x|＞

1

4

，可以先根据变量x的范围去绝对值，再解相应的不等式即可．

解答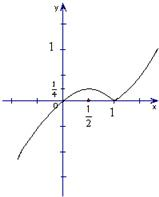：解：（Ⅰ）由f（1）=|m-1|=0?m=1．
∴f（x）=x|1-x|=

-x2+x，x≤1 x2-x，x＞1.

所以函数f（x）的解析式为：f（x）=

-x2+x，x≤1 x2-x，x＞1

．


（Ⅱ）图象如图：
∴函数f（x）的单调递增区间是(-∞，

1

2

]和[1，+∞），f（x）的单调递减区间是[

1

2

，1]；
（Ⅲ）由（Ⅱ）知，函数f（x）=-x²+x在区间（-∞，1）上的最大值为f(

1

2

)=

1

4

，
又∵函数f（x）=x²-x在区间（1，+∞）上单调递增，
如图可知，在区间（1，+∞）上存在x₀，有f（x₀）=

1

4

．
即令x²-x=

1

4

，解得x=

1± 2

2

．
又∵x∈（1，+∞），
∴x₀=

1+ 2

2

．
∴不等式f（x）＞

1

4

的解集是(

1+ 2

2

，+∞)．

解法二：∵x|1-x|＞

1

4

，
∴

x≤1 -x2+x＞ 1 4

①
或

x＞1 x2-x＞ 1 4

②
解①此不等式组无解，解②x＞

1+ 2

2

．
∴不等式f（x）＞

1

4

的解集是(

1+ 2

2

，+∞)．

点评：本题考查的是分段函数问题．在解答的过程当中充分体现了分类讨论的思想、数形结合的思想、函数与方程的思想以及问题转化的思想．值得同学们体会和反思．