题目内容
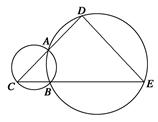
如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.
(1)求证A,I,H,E四点共圆;
(2)若∠C=50°,求∠IEH的度数.
(1)见解析 (2) 25°
解析解:(1)由圆I与AC相切于点E得IE⊥AC,结合HI⊥AH,得∠AEI=∠AHI=90°,所以A,I,H,E四点共圆.
(2)由(1)知A,I,H,E四点共圆,所以∠IEH=∠HAI.由题意知∠HIA=∠ABI+∠BAI=
∠ABC+∠BAC=(∠ABC+∠BAC)=(180°-∠C)=90°-∠C,结合IH⊥AH,得∠HAI=90°-∠HIA=90°-(90°-∠C)=∠C,所以∠IEH=∠C.由∠C=50°得∠IEH=25°.
练习册系列答案
相关题目
，延长CE交AB于点F，求△BCF外接圆的半径．
AC,AE=
AB,BD,CE相交于点F.
，求MA及CE的长．
