题目内容
已知函数f（x）=x2+ax+3在区间［-1，1］上的最小值m为-3，求实数a的取值.
解析：所给二次函数的对称轴x=-
是变化的，而区间是固定的，因而只需确定二次函数对称轴与区间的关系，即可求得a的范围.
解：f（x）=（x+
）2+3-
，开口向上，区间［-1，1］确定，对称轴x=-
随a变化.
（1）当-
＜-1，即a＞2时，作草图（Ⅰ）.
f（x）在［-1，1］上是增函数，所以m=f（-1）=-3，得1-a+3=-3.
所以a=7.
（2）当-
＞1，即a＜-2时，作草图（Ⅱ）.
f（x）在［-1，1］上是减函数，m=f（1）=1+a+3=-3，
所以a=-7.
（3）当-1≤-
≤1，即-2≤a≤2时，作草图（Ⅲ）.此时，对称轴在区间［-1，1］内，所以m=f（-
）=3-
=-3，得a=±2
，这与-2≤a≤2矛盾，舍去.因此所求的实数a=-7或7.
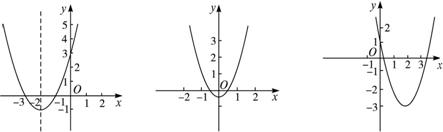
（Ⅰ） （Ⅱ） （Ⅲ）.
练习册系列答案
新编小学单元自测题系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|