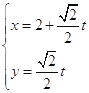Question

【题目】已知圆锥曲线 （ 为参数）和定点 ， F1 、 F2 是此圆锥曲线的左、右焦点，以原点 O 为极点，以 x 轴的正半轴为极轴建立极坐标系．
（1）求直线 AF2 的直角坐标方程；
（2）经过点 F1 且与直线AF2 垂直的直线 l 交此圆锥曲线于M,N 两点，求||MF1|-|NF1|| 的值．

Answer 1

【答案】
（1）

.

（2）

【解析】1.曲线 可化为 ，
其轨迹为椭圆，焦点为 F1(-1,0),F2(1,0) .
经过 和F2(1,0) 的直线方程为 ,即 .
2.由（1）知，直线 AF2 的斜率为 ，因为 ，所以l的斜率为 ，倾斜角为 ，
所以l的参数方程为 （t为参数），
代入椭圆C的方程中，得
因为M,N在点 F1 的两侧，所以 .
【考点精析】本题主要考查了椭圆的参数方程的相关知识点，需要掌握椭圆的参数方程可表示为才能正确解答此题．