题目内容
17.同学们经过市场调查,得出了某种商品在2013年的价格y(单位:元)与时间t(单位:月)的函数关系为y=2+$\frac{{t}^{2}}{20-t}$(1≤t≤12),则10月份该商品价格上涨的速度是3元/月.分析 根据导数的几何意义,求出函数的导数即可得到结论.
解答 解:∵y=2+$\frac{{t}^{2}}{20-t}$(1≤t≤12),
∴函数的导数y′=(2+$\frac{{t}^{2}}{20-t}$)′=($\frac{{t}^{2}}{20-t}$)′=$\frac{2t•(20-t)-{t}^{2}•(-1)}{(20-t)^{2}}$=$\frac{40t-{t}^{2}}{(20-t)^{2}}$,
由导数的几何意义可知10月份该商品价格上涨的速度为$\frac{40×10-1{0}^{2}}{(20-10)^{2}}=\frac{300}{100}=3$,
故答案为:3.
点评 本题主要考查导数的计算,求出函数的导数是解决本题的关键.

练习册系列答案
相关题目
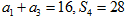
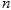 取何值时Sn最大,并求出这个最大值
取何值时Sn最大,并求出这个最大值