题目内容
函数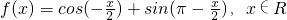 .
.
(1)求函数f(x)的对称轴方程;
(2)求f(x)在[0,π]上的减区间.
解:由题意
(1)令相位 ,解得,函数的对称轴方程为:
,解得,函数的对称轴方程为: …(4分)
…(4分)
(2)令 ,解得
,解得 ,
,
即函数的递减区间是
故f(x)在[0,π]上的减区间为: …(5分)
…(5分)
分析:可先对函数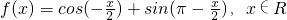 进行化简,得到
进行化简,得到
(1)由正弦函数的性质令相位 ,解出x即可得到对称轴方程;
,解出x即可得到对称轴方程;
(2)由正弦函数的性质令 解出x的范围,再与[0,π]取交集得到f(x)在[0,π]上的减区间
解出x的范围,再与[0,π]取交集得到f(x)在[0,π]上的减区间
点评:本题考查正弦函数的单调性,解题的关键是熟练掌握正弦函数的性质--单调性、图象的对称性,本题是三角函数基本性质考查题,其设计的主要目的是考查基本知识与基本技能的掌握情况.正弦函数的性质也是近几年高考的热点,熟练掌握、灵活运用方能正确快速解答出此类题.

(1)令相位
 ,解得,函数的对称轴方程为:
,解得,函数的对称轴方程为: …(4分)
…(4分)(2)令
 ,解得
,解得 ,
,即函数的递减区间是

故f(x)在[0,π]上的减区间为:
 …(5分)
…(5分)分析:可先对函数
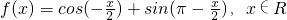 进行化简,得到
进行化简,得到
(1)由正弦函数的性质令相位
 ,解出x即可得到对称轴方程;
,解出x即可得到对称轴方程;(2)由正弦函数的性质令
 解出x的范围,再与[0,π]取交集得到f(x)在[0,π]上的减区间
解出x的范围,再与[0,π]取交集得到f(x)在[0,π]上的减区间点评:本题考查正弦函数的单调性,解题的关键是熟练掌握正弦函数的性质--单调性、图象的对称性,本题是三角函数基本性质考查题,其设计的主要目的是考查基本知识与基本技能的掌握情况.正弦函数的性质也是近几年高考的热点,熟练掌握、灵活运用方能正确快速解答出此类题.

练习册系列答案
相关题目
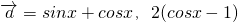 ,
,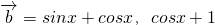 ,函数
,函数 .
.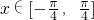 时,求函数f(x)的值域.
时,求函数f(x)的值域.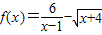 .
.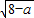
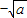 =0,求a的值.
=0,求a的值.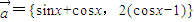 ,
,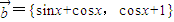 ,函数
,函数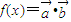 .
.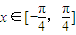 时,求函数f(x)的值域.
时,求函数f(x)的值域.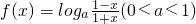 .
.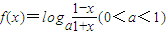 .
.