Question

设x=1是函数f(x)=e^-ax的一个极值点(a＞0,e为自然对数的底数).

(1)求a与b的关系式(用a表示b),并求函数f(x)的单调区间;

(2)若f(x)在闭区间［m,m+1］上的最小值为0,最大值为e^-a,且m≥0.试求实数m与a的值.

Answer 1

解:(1)f(x)的定义域为(-∞,-1)∪(-1,+∞),

∵f′(x)=-ae^-ax·+e^-ax·=e^-ax,

∴a+(ab+a)+ab+b-1=0.∴b=.

f′(x)=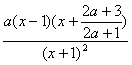e^-ax,令f′(x)=0,得x₁=1,x₂=,

∵a＞0,∴x₂＜-1.当x变化时f′(x),f(x)的变化情况如下表:

x	(-∞,x2)	(x2,-1)	(-1,1)	(1,+∞)
f′(x)	-	+	+	-
f(x)	减函数	增函数	增函数	减函数

    从上表可知:f(x)在区间(-∞,)和(1,+∞)上是减函数;

f(x)在区间(,-1)和(-1,1)上是增函数.

(2)①当m≥1时,f(x)在闭区间［m,m+1］上是减函数.

又x≥1时,f(x)=e^-ax=e^-ax＞0,

其最小值不可能为0,故此时的a,m也不存在.

②当0≤m＜1时,m+1∈［1,2),f(x)在(m,1］上是增函数,在［1,m+1］上是减函数.

则最大值为f(1)=e^-a=e^-a,得b=0,a=.

又f(m+1)＞0,f(x)的最小值为f(m)=0,

∴m=-b=0.综上可知m=0,a=.