题目内容
已知数列{an}中,a1=2,an-an-1-2n=0(n≥2,n∈N).
(1)写出a2、a3的值(只写结果)并求出数列{an}的通项公式;
(2)设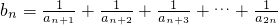 ,若对任意的正整数n,当m∈[-1,1]时,不等式
,若对任意的正整数n,当m∈[-1,1]时,不等式 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
解:(1)∵a1=2,an-an-1-2n=0(n≥2,n∈N)∴a2=6,a3=12(2分)
当n≥2时,an-an-1=2n,an-1-an-2=2(n-1),…,a3-a2=2×3,a2-a1=2×2,
∴an-a1=2[n+(n-1)+…+3+2],
∴ (5分)
(5分)
当n=1时,a1=1×(1+1)=2也满足上式,
∴数列{an}的通项公式为an=n(n+1)(6分)
(2) =
= =
= (8分)
(8分)
令 ,则
,则 ,当x≥1时,f'(x)>0恒成立
,当x≥1时,f'(x)>0恒成立
∴f(x)在x∈[1,+∞)上是增函数,故当x=1时,f(x)min=f(1)=3
即当n=1时, (11分)
(11分)
要使对任意的正整数n,当m∈[-1,1]时,不等式 恒成立,
恒成立,
则须使 ,
,
即t2-2mt>0,
对?m∈[-1,1]恒成立,
∴ ,
,
∴实数t的取值范围为(-∞,-2)∪(2,+∞)(14分)
分析:(1)由题设知a2=6,a3=12,an-an-1=2n,an-1-an-2=2(n-1),…,a3-a2=2×3,a2-a1=2×2,所以an-a1=2[n+(n-1)+…+3+2],由此可知数列{an}的通项公式为an=n(n+1).
(2)由题设条件可推出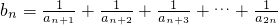 =
= ,令
,令 ,则
,则 ,当x≥1时,f'(x)>0恒成立,f(x)在x∈[1,+∞)上是增函数,故f(x)min=f(1)=3,
,当x≥1时,f'(x)>0恒成立,f(x)在x∈[1,+∞)上是增函数,故f(x)min=f(1)=3, ,
,
要使对任意的正整数n,当m∈[-1,1]时,不等式 恒成立,则须使
恒成立,则须使 ,即t2-2mt>0,对?m∈[-1,1]恒成立,由此可知实数t的取值范围.
,即t2-2mt>0,对?m∈[-1,1]恒成立,由此可知实数t的取值范围.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意公式的灵活运用.
当n≥2时,an-an-1=2n,an-1-an-2=2(n-1),…,a3-a2=2×3,a2-a1=2×2,
∴an-a1=2[n+(n-1)+…+3+2],
∴
 (5分)
(5分)当n=1时,a1=1×(1+1)=2也满足上式,
∴数列{an}的通项公式为an=n(n+1)(6分)
(2)
 =
= =
= (8分)
(8分)令
 ,则
,则 ,当x≥1时,f'(x)>0恒成立
,当x≥1时,f'(x)>0恒成立∴f(x)在x∈[1,+∞)上是增函数,故当x=1时,f(x)min=f(1)=3
即当n=1时,
 (11分)
(11分)要使对任意的正整数n,当m∈[-1,1]时,不等式
 恒成立,
恒成立,则须使
 ,
,即t2-2mt>0,
对?m∈[-1,1]恒成立,
∴
 ,
,∴实数t的取值范围为(-∞,-2)∪(2,+∞)(14分)
分析:(1)由题设知a2=6,a3=12,an-an-1=2n,an-1-an-2=2(n-1),…,a3-a2=2×3,a2-a1=2×2,所以an-a1=2[n+(n-1)+…+3+2],由此可知数列{an}的通项公式为an=n(n+1).
(2)由题设条件可推出
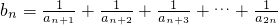 =
= ,令
,令 ,则
,则 ,当x≥1时,f'(x)>0恒成立,f(x)在x∈[1,+∞)上是增函数,故f(x)min=f(1)=3,
,当x≥1时,f'(x)>0恒成立,f(x)在x∈[1,+∞)上是增函数,故f(x)min=f(1)=3, ,
,要使对任意的正整数n,当m∈[-1,1]时,不等式
 恒成立,则须使
恒成立,则须使 ,即t2-2mt>0,对?m∈[-1,1]恒成立,由此可知实数t的取值范围.
,即t2-2mt>0,对?m∈[-1,1]恒成立,由此可知实数t的取值范围.点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答,注意公式的灵活运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|