题目内容
已知∠ABC=90°，PA⊥面ABC，若PA=AB=BC=1，E为PC的中点，则异面直线BE与AC所成的角为（ ）
| A、30° | B、45° | C、60° | D、90° |
分析：取PA的中点 M，连接ME，∠BEM 为异面直线成的角，把此角放在一个三角形中，解此三角形，求出异面直线成的角．
解答：解：∵∠ABC=90°，PA⊥面ABC，
若PA=AB=BC=1，E为PC的中点，
∴AC=
，PC=
，
∴BE=PE=
，
取PA的中点 M，连接ME，ME=
，BM=
，
∴∠BEM=90°．
故答案选 D．
若PA=AB=BC=1，E为PC的中点，
∴AC=
| 2 |
| 3 |
∴BE=PE=
| ||
| 2 |
取PA的中点 M，连接ME，ME=
| ||
| 2 |
| ||
| 2 |
∴∠BEM=90°．
故答案选 D．
点评：本题考查异面直线所成的角的求法．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
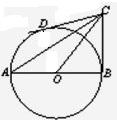如图，在Rt△ABC中，已知∠ABC=90°，BC=6，以AB为直径作⊙O，连接OC，过点C作⊙O的切线CD，D为切点，若sin∠OCD=
如图，在底面是直角梯形的四棱锥S-ABCD中，已知∠ABC=90°，SA⊥平面ABCD，AB=BC=2，AD=1．