题目内容
 如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.
如图,在底面是直角梯形的四棱锥S-ABCD中,已知∠ABC=90°,SA⊥平面ABCD,AB=BC=2,AD=1.(1)当SA=2时,求直线SA与平面SCD所成角的正弦值;
(2)若平面SCD与平面SAB所成角的余弦值为
| 4 | 9 |
分析:(1)建立空间直角坐标系,求出SCD 的法向量
,利用
与
夹角余弦得值去解决.
(2)求出平面SCD与平面SAB 的法向量
,
,利用面SCD与平面SAB所成角与
,
的夹角相等或互补的关系去解决.
| n |
| SA |
| n |
(2)求出平面SCD与平面SAB 的法向量
| n |
| m |
| n |
| m |
解答: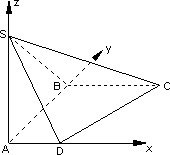 解:以A为原点,建立如图所示空间直角坐标系.
解:以A为原点,建立如图所示空间直角坐标系.
各点坐标 A(0,0,0)S(0,0,2)D(1,0,0)C(2,2,0)
=(1,0,-2)
=(2,2,-2),
设面SCD的一个法向量为
=(x,y,z),
则
即
取z=1.则
=(2,-1,1)
又
=(0,0,2)
|cos<
,
>=
=
=
.∴直线SA与平面SCD所成角的正弦值等于
.
(2)设SA=a,则 S(0,0,a),
=(1,0,-a)
=(2,2,-a),
设面SCD的一个法向量为
=(x,y,z),则
即
取z=1.则
=(a,-
,1)
又面SAB的一个法向量为
=(1,0,0),|cos<
,
>|=
=
=
,解得a=
 解:以A为原点,建立如图所示空间直角坐标系.
解:以A为原点,建立如图所示空间直角坐标系.| n |
各点坐标 A(0,0,0)S(0,0,2)D(1,0,0)C(2,2,0)
| SD |
| SC |
设面SCD的一个法向量为
| n |
则
|
|
| n |
又
| AS |
|cos<
| n |
| AS |
|
| ||||
|
|
| 2 | ||
|
| ||
| 6 |
| ||
| 6 |
(2)设SA=a,则 S(0,0,a),
| SD |
| SC |
设面SCD的一个法向量为
| n |
|
|
| n |
| a |
| 2 |
又面SAB的一个法向量为
| m |
| m |
| n |
|
| ||||
|
|
| a | ||||
|
| 4 |
| 9 |
4
| ||
| 61 |
点评:本题考用空间向量解决直线和平面位置关系、二面角大小,考查转化的思想方法,空间想象能力,计算能力.属于常规题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
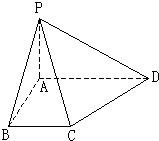 如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且
如图,在底面是直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,且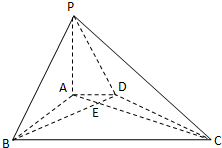 如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB=
如图,在底面是直角梯形的四棱锥 P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=4.AD=2,AB= (2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
(2012•宿州一模)如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.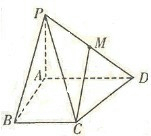 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面 ABCD,PA=AB=BC=1,AD=2,M为PD中点.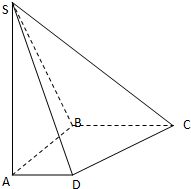 如图,在底面是直角梯形的四棱锥S-ABCD中,
如图,在底面是直角梯形的四棱锥S-ABCD中,