题目内容
 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=| 2 |
(Ⅰ)求证:AF∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面BCE.
(Ⅲ)求凸多面体ABCED的体积.
分析:(I)作BE的中点G,连接GF,GD,由三角形中位线定理,及平行四边形判定定理可得四边形GFAD为平行四边形,进而AF∥GD,再由线面平行的判定定理得到AF∥平面BDE;
(Ⅱ)由AB=AC,F为BC的中点可得AF⊥BC,结合GF⊥AF及线面垂直的判定定理可得AF⊥平面BCE进而由面面垂直的判定定理得到平面BDE⊥平面BCE.
(Ⅲ)由已知可判断四边形ACED为梯形,且平面ABC⊥平面ACED,由面面垂直的性质定理可得AB⊥平面ACED,即AB为四棱锥B-ACED的高,代入棱锥体积公式可得答案.
(Ⅱ)由AB=AC,F为BC的中点可得AF⊥BC,结合GF⊥AF及线面垂直的判定定理可得AF⊥平面BCE进而由面面垂直的判定定理得到平面BDE⊥平面BCE.
(Ⅲ)由已知可判断四边形ACED为梯形,且平面ABC⊥平面ACED,由面面垂直的性质定理可得AB⊥平面ACED,即AB为四棱锥B-ACED的高,代入棱锥体积公式可得答案.
解答: 证明:(Ⅰ)作BE的中点G,连接GF,GD,∴GF为三角形BCE的中位线,
证明:(Ⅰ)作BE的中点G,连接GF,GD,∴GF为三角形BCE的中位线,
∴GF∥EC∥DA,GF=
CE=DA,…(5分)
∴四边形GFAD为平行四边形,
∴AF∥GD,又GD?平面BDE,∴AF∥平面BDE.…(7分)
(Ⅱ)∵AB=AC,F为BC的中点,
∴AF⊥BC,又GF⊥AF,∴AF⊥平面BCE,…(10分)
∵AF∥GD,∴GD⊥平面BCE,又GD?平面BDE,
∴平面BDE⊥平面BCE. …(12分)
(Ⅲ)∵AD⊥平面ABC,CE⊥平面ABC,∴四边形ACED为梯形,且平面ABC⊥平面ACED,∵BC2=AC2+AB2,∴AB⊥AC,…(1分)
∵平面ABC∩平面ACED=AC,∴AB⊥平面ACED,
即AB为四棱锥B-ACED的高,…(2分)
∴VB-ACED=
•SACED•AB=
×
×(1+CE)×1×1=
 证明:(Ⅰ)作BE的中点G,连接GF,GD,∴GF为三角形BCE的中位线,
证明:(Ⅰ)作BE的中点G,连接GF,GD,∴GF为三角形BCE的中位线,∴GF∥EC∥DA,GF=
| 1 |
| 2 |
∴四边形GFAD为平行四边形,
∴AF∥GD,又GD?平面BDE,∴AF∥平面BDE.…(7分)
(Ⅱ)∵AB=AC,F为BC的中点,
∴AF⊥BC,又GF⊥AF,∴AF⊥平面BCE,…(10分)
∵AF∥GD,∴GD⊥平面BCE,又GD?平面BDE,
∴平面BDE⊥平面BCE. …(12分)
(Ⅲ)∵AD⊥平面ABC,CE⊥平面ABC,∴四边形ACED为梯形,且平面ABC⊥平面ACED,∵BC2=AC2+AB2,∴AB⊥AC,…(1分)
∵平面ABC∩平面ACED=AC,∴AB⊥平面ACED,
即AB为四棱锥B-ACED的高,…(2分)
∴VB-ACED=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查的知识点是平面与平面垂直的判定,棱锥的体积,直线与平面平行的判定,其中(I)的关键是得到四边形GFAD为平行四边形,(II)的关键是证得GD⊥平面BCE,(III)的关键是计算出棱锥的底面面积及高.

练习册系列答案
相关题目
 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1, 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC= 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,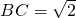 ,CE=2,F为BC的中点.
,CE=2,F为BC的中点. 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1, ,凸多面体ABCED的体积为
,凸多面体ABCED的体积为 ,F为BC的中点.
,F为BC的中点.