题目内容
 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,BC=| 2 |
(1)求证:平面BED⊥平面BCE;
(2)求凸多面体ABCED的体积.
分析:(1)取BE的中点G,连结DG、FG,利用等腰三角形“三线合一”证出AF⊥BC,根据三角形中位线定理结合线面垂直的判定与性质证出GF⊥AF,从而得出AF⊥平面BEC,由DG∥AF得DG⊥平面BEC,再根据面面垂直的定理即可证出平面BED⊥平面BCE;
(2)根据EC⊥平面ABC,利用面面垂直的判定证出平面ACDE⊥平面ABC,由勾股定理的逆定理证出AB⊥AC,根据面面垂直的性质得AB⊥平面ACDE,可得AB为四棱锥B-ACED的高.算出直角梯形ACED的面积,并利用锥体的体积公式算出四棱锥B-ACED的体积,即可得出凸多面体ABCED的体积.
(2)根据EC⊥平面ABC,利用面面垂直的判定证出平面ACDE⊥平面ABC,由勾股定理的逆定理证出AB⊥AC,根据面面垂直的性质得AB⊥平面ACDE,可得AB为四棱锥B-ACED的高.算出直角梯形ACED的面积,并利用锥体的体积公式算出四棱锥B-ACED的体积,即可得出凸多面体ABCED的体积.
解答:解:(1)取BE的中点G,连结DG、FG,
∵AB=AC=1,F为BC的中点,∴AF⊥BC.
∵GF是△BCE的中位线,∴EC∥GF,
∵EC⊥平面ABC,∴GF⊥平面ABC.
又∵AF?平面ABC,∴GF⊥AF.
∵GF∩BC=F,∴AF⊥平面BCE.
∵AF∥DG,∴DG⊥平面BCE.
又∵DG?平面BDE,∴平面BDE⊥平面BCE;
(2)∵AD⊥平面ABC,EC⊥平面ABC,∴四边形ACED为直角梯形;
∵EC?平面ACDE,EC⊥平面ABC,∴平面ACDE⊥平面ABC,
∵AC2+AB2=2=BC2,∴∠BAC=90°,可得AB⊥AC,
∵AB?平面ABC,平面ACDE∩平面ABC,
∴AB⊥平面ACDE,可得AB为四棱锥B-ACED的高.
由此可得VB-ACED=
×SABCD×AB=
×
×(1+2)×1×1=
,即凸多面体ABCED的体积为
.
∵AB=AC=1,F为BC的中点,∴AF⊥BC.

∵GF是△BCE的中位线,∴EC∥GF,
∵EC⊥平面ABC,∴GF⊥平面ABC.
又∵AF?平面ABC,∴GF⊥AF.
∵GF∩BC=F,∴AF⊥平面BCE.
∵AF∥DG,∴DG⊥平面BCE.
又∵DG?平面BDE,∴平面BDE⊥平面BCE;
(2)∵AD⊥平面ABC,EC⊥平面ABC,∴四边形ACED为直角梯形;
∵EC?平面ACDE,EC⊥平面ABC,∴平面ACDE⊥平面ABC,
∵AC2+AB2=2=BC2,∴∠BAC=90°,可得AB⊥AC,
∵AB?平面ABC,平面ACDE∩平面ABC,
∴AB⊥平面ACDE,可得AB为四棱锥B-ACED的高.
由此可得VB-ACED=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题给出凸多面体满足的条件,求证面面垂直并求锥体的体积.着重考查了线面垂直、面面垂直的判定与性质和锥体体积公式等知识,属于中档题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1, 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1, 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,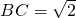 ,CE=2,F为BC的中点.
,CE=2,F为BC的中点. 如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1,
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1, ,凸多面体ABCED的体积为
,凸多面体ABCED的体积为 ,F为BC的中点.
,F为BC的中点.