题目内容
6.已知{an}为等差数列,a1=-12,a5=2a6.(I)求数列{an}的通项公式以及前n项和Sn.
(Ⅱ)求使得Sn>14的最小正整数n的值.
分析 (Ⅰ)利用等差数列通项公式求出公差d=2,由此能求出数列{an}的通项公式以及前n项和Sn.
(Ⅱ)由Sn>14,得${S}_{n}={n}^{2}-13n>14$,且n∈N*,由此能求出使得Sn>14的最小正整数n的值为15.
解答 解:(Ⅰ)∵{an}为等差数列,a1=-12,a5=2a6.
∴-12+4d=2(-12+5d),
解得d=2,
∴an=-12+(n-1)×2=2n-14.
Sn=$-12n+\frac{n(n-1)}{2}×2$=n2-13n.
(Ⅱ)∵Sn>14,∴${S}_{n}={n}^{2}-13n>14$,且n∈N*,
解得n>14,且n∈N*,
∴使得Sn>14的最小正整数n的值为15.
点评 本题考查等差数列的通项公式及前n项和的求法,考查满足数列的前14项和的最小正整数n的值的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
16.如果圆x2+y2+2m(x+y)+2m2-8=0上总存在到点(0,0)的距离为$\sqrt{2}$的点,则实数m的取值范围是( )
| A. | [-1,1] | B. | (-3,3) | C. | (-3,-1)∪(1,3) | D. | [-3,-1]∪[1,3] |
17.在下列四个图中,每个图的两个变量具有相关关系的图是( )


| A. | (1)(2) | B. | (1)(3) | C. | (2)(4) | D. | (2)(3) |
14.根据下表提供的数据,由散点图可知,y与x具有较好的线性相关关系,其线性回归方程为$\widehat{y}$=-0.7x+5.25,那么表中t的值为( )
| x | 1 | 2 | 3 | 4 |
| y | 4.5 | 4 | t | 2.5 |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
1.sin43°cos17°+cos43°sin17°的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
18.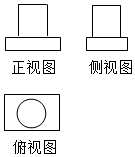 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
 如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )
如图是某几何体的三视图,则此几何体可由下列哪两种几何体组合而成( )| A. | 两个长方体 | B. | 两个圆柱 | ||
| C. | 一个长方体和一个圆柱 | D. | 一个球和一个长方体 |
15. 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )| A. | $\frac{π}{2}+1$ | B. | $\frac{π}{2}+3$ | C. | $\frac{3π}{2}+1$ | D. | $\frac{3π}{2}+3$ |