题目内容
如图三棱柱ABC-A1B1C1中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC1中点,AB1与A1B交于点O。
(I)求证:CD//平面A1EB。
(II)求证:平面AB1C⊥平面A1EB
 |
证明:(I)∵ 棱柱的每个侧面为正方形
![]() ∴AA1⊥AC
∴AA1⊥AC
AA1⊥AB
∴三棱柱为正三棱柱
连OD,∵D为AB中点,O为对面线AB1,A1B交点
∴OD//![]() BB1
BB1
又E为CC1中点 ∴EC//![]() BB1
BB1
OD//EC
DCEO为平行四边形 CD//EO
CD![]() 平面A1EB EO
平面A1EB EO![]() 平面A1EB ∴CD//平面A1EB
平面A1EB ∴CD//平面A1EB
(II)∵ AB=AC=CB
∴ CD⊥AB
又直棱柱侧面ABB1A1⊥底面ABC
∴CD⊥平面ABB1A1 CD⊥AB1
由(I)CD//EO ∴EO⊥AB1
又正方形中 A1B⊥AB1
EO![]() A1B=0, EO A1B
A1B=0, EO A1B![]() 平面A1EB
平面A1EB
∴AB1⊥平面A1EB
AB1![]() 平面AB1C ∴平面A1EB⊥平面AB1C
平面AB1C ∴平面A1EB⊥平面AB1C

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 如图三棱柱ABC-A1B1C1中,侧棱BB1与底面成60.角,AQ⊥底面A1B1C1于Q,AP⊥侧面BCC1B1于P,且A1Q⊥B1C1,AB=AC,AQ=3,AP=2则顶点A到棱B1C1的距离是
如图三棱柱ABC-A1B1C1中,侧棱BB1与底面成60.角,AQ⊥底面A1B1C1于Q,AP⊥侧面BCC1B1于P,且A1Q⊥B1C1,AB=AC,AQ=3,AP=2则顶点A到棱B1C1的距离是 如图三棱柱ABC-A1B1C1中,E,F分别是AB、AC的中点,平面EFC1B1将三棱柱分成体积为V1,V2(左为V1,右为V2)两部分,则V1:V2=( )
如图三棱柱ABC-A1B1C1中,E,F分别是AB、AC的中点,平面EFC1B1将三棱柱分成体积为V1,V2(左为V1,右为V2)两部分,则V1:V2=( )| A、7:5 | B、4:3 | C、3:1 | D、2:1 |
 某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图三棱柱ABC-A1B1C1的六个顶点上各安装一个灯泡,要求同一条线段的两端的灯泡颜色不同,则每种颜色的灯泡至少用一个的安装方法共有( )
某人有4种颜色的灯泡(每种颜色的灯泡足够多),要在如图三棱柱ABC-A1B1C1的六个顶点上各安装一个灯泡,要求同一条线段的两端的灯泡颜色不同,则每种颜色的灯泡至少用一个的安装方法共有( )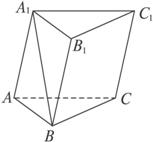
 , 若存在, 求CE的长, 若不存在,
, 若存在, 求CE的长, 若不存在,