Question

方程

x2-1

=x+m有实数解，则实数m的取值范围是

 

．

Answer 1

分析：由y=

x2-1

，化为x²-y²=1（y≥0），其渐近线为y=±x．分别画出函数y=

x2-1

，y=x+m的图象．可得直线y=x+m与y轴的交点M（0，-1），N（0，1）．即可得出m的取值范围．

解答：解：由y=

x2-1

，化为x²-y²=1（y≥0），其渐近线为y=±x．
分别画出函数y=

x2-1

，y=x+m的图象．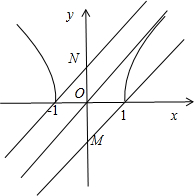
可得直线y=x+m与y轴的交点M（0，-1），N（0，1）．
由图象可得：当-1≤m＜0或m≥1时，函数y=

x2-1

，y=x+m的图象有交点，即方程

x2-1

=x+m有实数解．
实数m的取值范围是-1≤m＜0或m≥1．
故答案为：[-1，0）∪[1，+∞）．

点评：本题考查了双曲线的标准方程及其性质、直线的方程、数形结合等基础知识与基本技能方法，属于难题．