题目内容
（2012•闵行区一模）设x1、x2是关于x的方程x2+mx+m2-m=0的两个不相等的实数根，那么过两点A（x1，x12），B（x2，x22）的直线与圆（x-1）2+y2=1的位置关系是（ ）
分析：由已知的一元二次方程有两个不相等的实数根，得到根的判别式大于0，列出关于m的不等式，求出不等式的解集得到m的范围，再利用根与系数的关系表示出两根之和，由A和B坐标的特点得到这两点在抛物线y=x2上，且根据两点的坐标求出直线AB的斜率，化简后将表示出的两根之和代入得到关于m的式子，在同一个坐标系中画出圆与抛物线，由图象可知直线AB与圆的位置关系不确定，随m的变化而变化．
解答：解：∵x1、x2是关于x的方程x2+mx+m2-m=0的两个不相等的实数根，
∴m2-4（m2-m）＞0，即0＜m＜
，
∴x1+x2=-m，
由A（x1，x12），B（x2，x22），得到A和B为抛物线y=x2上的两点，
且直线AB的斜率k=
=x1+x2=-m，又圆心坐标为（1，0），半径r=1，
在同一个坐标系中作出相应的图形，如图所示：
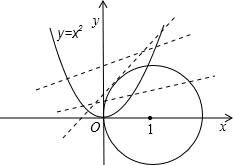
则直线AB与圆（x-1）2+y2=1的位置关系可能相交、相切或相离，由m的值变化而变化．
故选D
∴m2-4（m2-m）＞0，即0＜m＜
| 4 |
| 3 |
∴x1+x2=-m，
由A（x1，x12），B（x2，x22），得到A和B为抛物线y=x2上的两点，
且直线AB的斜率k=
| x22-x12 |
| x2-x1 |
在同一个坐标系中作出相应的图形，如图所示：
则直线AB与圆（x-1）2+y2=1的位置关系可能相交、相切或相离，由m的值变化而变化．
故选D
点评：此题考查了直线与圆的位置关系，涉及的知识有：韦达定理，直线斜率的求法，以及圆的标准方程，利用了数形结合的思想，数形结合思想是数学中重要的思想方法，做题时要灵活运用．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
（2012•闵行区一模）在一圆周上给定1000个点．（如图）取其中一点标记上数1，从这点开始按顺时针方向数到第二个点标记上数2，从标记上2的点开始按顺时针方向数到第三个点标记上数3，继续这个过程直到1，2，3，…，2012都被标记到点上，圆周上这些点中有些可能会标记上不止一个数，在标记上2012的那一点上的所有标记的数中最小的是
（2012•闵行区一模）将边长分别为1、2、3、…、n、n+1、…（n∈N*）的正方形叠放在一起，形成如图所示的图形，由小到大，依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形．容易知道第1个阴影部分图形的周长为8．设前n个阴影部分图形的周长的平均值为f（n），记数列{an}满足