题目内容
已知函数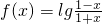
(1)求函数f(x)的定义域;
(2)证明函数f(x)为奇函数.
(1)解:∵由lg ,得出
,得出 >0,且1+x≠0
>0,且1+x≠0
∴有(1-x)>0且(1+x)>0或者(1-x)<0且(1+x)<0
∵解得第一个不等式有-1<x<1,第二个不等式不存在
∴函数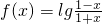 的定义域{x|-1<x<1}
的定义域{x|-1<x<1}
(2)证明∵f(-x)+f(x)=lg +lg
+lg =lg1=0
=lg1=0
∴f(x)=-f(-x)
∴函数f(x)为奇函数
分析:(1)由lg ,得
,得 >0,进而求出x的取值范围,得到答案.
>0,进而求出x的取值范围,得到答案.
(2)证明f(-x)+f(x)=0,进而证明f(x)=-f(-x)得出答案
点评:本题主要考查对数取值范围,求函数定义域.及利用f(x)=-f(-x)或f(x)=f(-x)证明函数奇偶性.
 ,得出
,得出 >0,且1+x≠0
>0,且1+x≠0∴有(1-x)>0且(1+x)>0或者(1-x)<0且(1+x)<0
∵解得第一个不等式有-1<x<1,第二个不等式不存在
∴函数
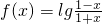 的定义域{x|-1<x<1}
的定义域{x|-1<x<1}(2)证明∵f(-x)+f(x)=lg
 +lg
+lg =lg1=0
=lg1=0∴f(x)=-f(-x)
∴函数f(x)为奇函数
分析:(1)由lg
 ,得
,得 >0,进而求出x的取值范围,得到答案.
>0,进而求出x的取值范围,得到答案.(2)证明f(-x)+f(x)=0,进而证明f(x)=-f(-x)得出答案
点评:本题主要考查对数取值范围,求函数定义域.及利用f(x)=-f(-x)或f(x)=f(-x)证明函数奇偶性.

练习册系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线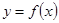 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)