题目内容
已知椭圆C的中心为原点O,点F(1,0)是它的一个焦点,直线l过点F与椭圆C交于A,B两点,当直线l垂直于x轴时, =
=
(I)求椭圆C的方程;
(II)已知点P为椭圆的上顶点,且存在实数t使
 成立,求实数t的值和直线l的方程.
成立,求实数t的值和直线l的方程.
【答案】分析:(I)设椭圆C的方程为 (a>b>0),则a2-b2=1,当l垂直于x轴时,A,B两点的坐标分别是(1,
(a>b>0),则a2-b2=1,当l垂直于x轴时,A,B两点的坐标分别是(1, )和(1,-
)和(1,- ),由
),由 =(1,
=(1, )•(1,-
)•(1,- )=1-
)=1- ,知a2=2b4,由此能求出椭圆C的方程.
,知a2=2b4,由此能求出椭圆C的方程.
(II)当直线斜率不存在时,A(1, ),B(1,-
),B(1,- ),P(0,1),
),P(0,1), =(1,
=(1, -1),
-1), =(1,-
=(1,- -1),
-1), =(1,-1),由t使
=(1,-1),由t使 ,得直线l的方程为x=1当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2),
,得直线l的方程为x=1当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2), =(x1,y1-1),
=(x1,y1-1), =(x2,y2-1),
=(x2,y2-1), =(1,-1),由t使
=(1,-1),由t使 +
+ =t
=t ,得直线l的方程为y=-x+1.由此能求出结果.
,得直线l的方程为y=-x+1.由此能求出结果.
解答:解:(I)设椭圆C的方程为 (a>b>0),
(a>b>0),
则a2-b2=1,①
∵当l垂直于x轴时,A,B两点的坐标分别是(1, )和(1,-
)和(1,- ),
),
∴ =(1,
=(1, )•(1,-
)•(1,- )=1-
)=1- ,
,
则1- =
= ,即a2=2b4.②
,即a2=2b4.②
由①,②消去a,得2b4-b2-1=0.∴b2=1或b2=- .
.
当b2=1时,a2=2.因此,椭圆C的方程为 .
.
(II)当直线斜率不存在时,A(1, ),B(1,-
),B(1,- ),P(0,1),
),P(0,1),
所以 =(1,
=(1, -1),
-1), =(1,-
=(1,- -1),
-1), =(1,-1),
=(1,-1),
由t使 ,得t=2,直线l的方程为x=1
,得t=2,直线l的方程为x=1
当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2),
所以, =(x1,y1-1),
=(x1,y1-1), =(x2,y2-1),
=(x2,y2-1), =(1,-1),
=(1,-1),
由t使 +
+ =t
=t ,得
,得
 ,即
,即 ,
,
因为y1=k(x1-1),y2=k(x2-1),
所以,y1+y2=k(x1+x2-2),解得:k=-1
此时,直线l的方程为y=-x+1,
联立 ,得3x2-4x=0,t=x1+x2=
,得3x2-4x=0,t=x1+x2= ,
,
∴当直线斜率存在时,t= ,直线l的方程为y=-x+1,
,直线l的方程为y=-x+1,
综上所述,存在实数t,且t=2时,直线方程x=1,
当t=1时,直线l的方程为y=-x+1.
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意分类讨论思想和等价转化思想的合理运用.
 (a>b>0),则a2-b2=1,当l垂直于x轴时,A,B两点的坐标分别是(1,
(a>b>0),则a2-b2=1,当l垂直于x轴时,A,B两点的坐标分别是(1, )和(1,-
)和(1,- ),由
),由 =(1,
=(1, )•(1,-
)•(1,- )=1-
)=1- ,知a2=2b4,由此能求出椭圆C的方程.
,知a2=2b4,由此能求出椭圆C的方程.(II)当直线斜率不存在时,A(1,
 ),B(1,-
),B(1,- ),P(0,1),
),P(0,1), =(1,
=(1, -1),
-1), =(1,-
=(1,- -1),
-1), =(1,-1),由t使
=(1,-1),由t使 ,得直线l的方程为x=1当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2),
,得直线l的方程为x=1当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2), =(x1,y1-1),
=(x1,y1-1), =(x2,y2-1),
=(x2,y2-1), =(1,-1),由t使
=(1,-1),由t使 +
+ =t
=t ,得直线l的方程为y=-x+1.由此能求出结果.
,得直线l的方程为y=-x+1.由此能求出结果.解答:解:(I)设椭圆C的方程为
 (a>b>0),
(a>b>0),则a2-b2=1,①
∵当l垂直于x轴时,A,B两点的坐标分别是(1,
 )和(1,-
)和(1,- ),
),∴
 =(1,
=(1, )•(1,-
)•(1,- )=1-
)=1- ,
,则1-
 =
= ,即a2=2b4.②
,即a2=2b4.②由①,②消去a,得2b4-b2-1=0.∴b2=1或b2=-
 .
.当b2=1时,a2=2.因此,椭圆C的方程为
 .
.(II)当直线斜率不存在时,A(1,
 ),B(1,-
),B(1,- ),P(0,1),
),P(0,1),所以
 =(1,
=(1, -1),
-1), =(1,-
=(1,- -1),
-1), =(1,-1),
=(1,-1),由t使
 ,得t=2,直线l的方程为x=1
,得t=2,直线l的方程为x=1当直线斜率存在时,设直线l的方程为y=k(x-1),A=(x1,y1),B=(x2,y2),
所以,
 =(x1,y1-1),
=(x1,y1-1), =(x2,y2-1),
=(x2,y2-1), =(1,-1),
=(1,-1),由t使
 +
+ =t
=t ,得
,得 ,即
,即 ,
,因为y1=k(x1-1),y2=k(x2-1),
所以,y1+y2=k(x1+x2-2),解得:k=-1
此时,直线l的方程为y=-x+1,
联立
 ,得3x2-4x=0,t=x1+x2=
,得3x2-4x=0,t=x1+x2= ,
,∴当直线斜率存在时,t=
 ,直线l的方程为y=-x+1,
,直线l的方程为y=-x+1,综上所述,存在实数t,且t=2时,直线方程x=1,
当t=1时,直线l的方程为y=-x+1.
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意分类讨论思想和等价转化思想的合理运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
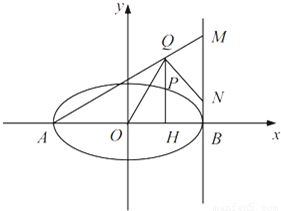
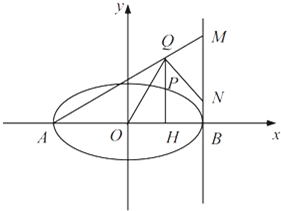 (2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为
(2013•深圳一模)已知椭圆C 的中心为原点O,焦点在x 轴上,离心率为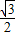 ,且点
,且点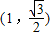 在该椭圆上.
在该椭圆上.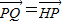 ,直线AQ与过点B 且垂直于x 轴的直线交于点M,
,直线AQ与过点B 且垂直于x 轴的直线交于点M,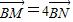 .求证:∠OQN为锐角.
.求证:∠OQN为锐角.