题目内容
设数列{an}是等差数列,bk=
(k∈N+).
(1) 求证:数列{ bn} 也是等差数列;
(2) 若a1=-2,
=
,求数列{an}、{bn} 的通项公式.
| a1+a2+…+ak |
| k |
(1) 求证:数列{ bn} 也是等差数列;
(2) 若a1=-2,
| a1+a2+…+a13 |
| b1+b2+…+b13 |
| 3 |
| 2 |
(1)设an=a1+(n-1)d,则bn=
=(a1-
)+
,
又bn+1-bn=
,
所以{bn}是以a1为首项,
为公差的等差数列;
(2)因为bn=a1+
d,且a1=-2,
则
=
=
=
,即-4+12d=-6+9d,
解得d=-
,
∴an=-
n-
,bn=-
n-
.
na1+
| ||
| n |
| d |
| 2 |
| nd |
| 2 |
又bn+1-bn=
| d |
| 2 |
所以{bn}是以a1为首项,
| d |
| 2 |
(2)因为bn=a1+
| n-1 |
| 2 |
则
| a1+a2+…+a13 |
| b1+b2+…+b13 |
| ||
|
| -2+6d |
| -2+3d |
| 3 |
| 2 |
解得d=-
| 2 |
| 3 |
∴an=-
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
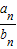 }的前n项和Sn.
}的前n项和Sn.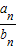 }的前n项和Sn.
}的前n项和Sn.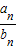 }的前n项和Sn.
}的前n项和Sn.