题目内容
对于给定数列{cn},如果存在实常数p、q,使得cn+1=pcn+q对于任意n∈N*都成立,我们称数列{cn}是“M类数列”;(1)若an=2n,数列{an}是否为“M类数列”?若是,指出它对应的实常数p、q,若不是,请说明理由;
(2)数列{an}满足a1=2,an+an+1=3•2n(n∈N*),若数列{an}是“M类数列”,求数列{an}的通项公式;
(3)记数列{an}的前n项之和为Sn,求证:
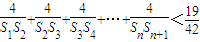 (n≥3).
(n≥3).
【答案】分析:(1)由an=2n,可得an+1=an+2,根据“M类数列”定义,可得结论;
(2)根据数列{an}是“M类数列”,可得存在实常数p、q使得an+1=pan+q对于任意n∈N*都成立,结合an+an+1=3•2n(n∈N*),可求数列{an}的通项公式;
(3)确定数列{an}的前n项之和为Sn,利用放缩法,结合裂项求和,即可得到结论.
解答:(1)解:∵an=2n,∴an+1=an+2,
故数列{an}是“M类数列”,对应的实常数p、q的值分别为1、2.(2分)
(2)解:∵数列{an}是“M类数列”,
∴存在实常数p、q使得an+1=pan+q对于任意n∈N*都成立,
∴an+2=pan+1+q,故(4分)
又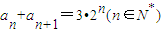 ,∴对于任意n∈N*都成立,
,∴对于任意n∈N*都成立,
即对于任意n∈N*都成立,(6分)
因此p=2,q=0
此时,∴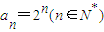 (8分)
(8分)
(3)证明:由(2)知: (9分)
(9分)
当n≥3时,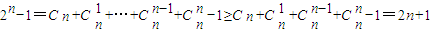 ,
,
当且仅当n=3时等号成立,所以Sn≥2(2n+1)(11分)
于是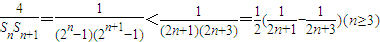
因为S1=2,S2=6,S3=14,所以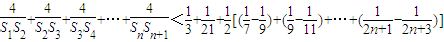
=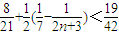 .(13分)
.(13分)
点评:本题考查新定义,考查数列与不等式的结合,考查数列的通项,考查放缩法、裂项法,属于中档题.
(2)根据数列{an}是“M类数列”,可得存在实常数p、q使得an+1=pan+q对于任意n∈N*都成立,结合an+an+1=3•2n(n∈N*),可求数列{an}的通项公式;
(3)确定数列{an}的前n项之和为Sn,利用放缩法,结合裂项求和,即可得到结论.
解答:(1)解:∵an=2n,∴an+1=an+2,
故数列{an}是“M类数列”,对应的实常数p、q的值分别为1、2.(2分)
(2)解:∵数列{an}是“M类数列”,
∴存在实常数p、q使得an+1=pan+q对于任意n∈N*都成立,
∴an+2=pan+1+q,故(4分)
又
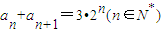 ,∴对于任意n∈N*都成立,
,∴对于任意n∈N*都成立,即对于任意n∈N*都成立,(6分)
因此p=2,q=0
此时,∴
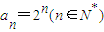 (8分)
(8分)(3)证明:由(2)知:
 (9分)
(9分)当n≥3时,
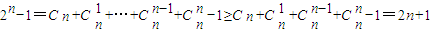 ,
,当且仅当n=3时等号成立,所以Sn≥2(2n+1)(11分)
于是
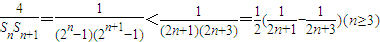
因为S1=2,S2=6,S3=14,所以
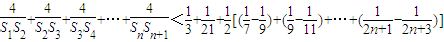
=
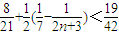 .(13分)
.(13分)点评:本题考查新定义,考查数列与不等式的结合,考查数列的通项,考查放缩法、裂项法,属于中档题.

练习册系列答案
相关题目