题目内容
函数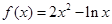
的递增区间是（ ）．
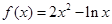的递增区间是（ ）．A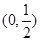． | B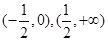． | C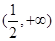． | D． |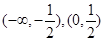
C
分析：先确定函数的定义域然后求导数fˊ（x），在函数的定义域内解不等式fˊ（x）＞0，即可求出函数
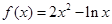的递增区间．解答：解：∵
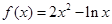，x＞0∴f’（x）=4x-
令f’（x）=4x-
＞0，解得x＞
∴函数
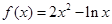的递增区间是（，+∞）故选C．
点评：本题主要考查了对数函数的导数，以及利用导数研究函数的单调性等基础知识，考查计算能力，属于基础题．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
。
，
；
(
)
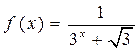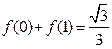
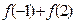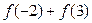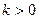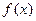的极值
．
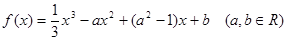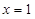为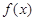
的极值点，求
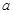的值；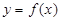
的图象在点（
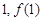）处的切线方程为
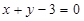，求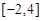
上的最大值；
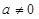时，若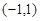
上不单调，求
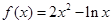的递增区间是（ ）．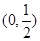
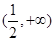
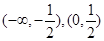
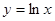是函数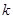
的值为（ ）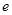
__________．
= .
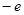
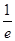
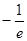
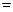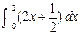