题目内容
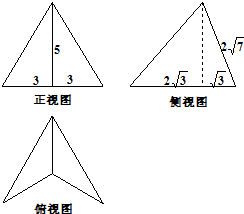（2012•安徽模拟）一个几何体的三视图及其有关数据如图所示，则这个几何体的体积是10
| 3 |
10
．| 3 |
分析：由三视图可得：原几何体是一个由两个全等的三棱锥P-ABD与P-BCD共一个侧面PBD所组成的，如图所示，PD⊥底面ABD，且PD=5，BD=2
，BD垂直平分AC，AC=6，PE=2
，DE=
据此即可计算出其体积．
| 3 |
| 7 |
| 3 |
解答：解：由三视图可得：原几何体是一个由两个全等的三棱锥P-ABD与P-BCD共一个侧面PBD所组成的，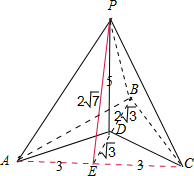
如图所示，PD⊥底面ABD，且PD=5，BD=2
，BD垂直平分AC，AC=6，PE=2
，DE=
．
∴V=2×
×
×2
×3×5=10
．
故答案为10
如图所示，PD⊥底面ABD，且PD=5，BD=2
| 3 |
| 7 |
| 3 |
∴V=2×
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
故答案为10
| 5 |
点评：由三视图正确恢复原几何体是解题的关键．注意该几何体的底面是由两个三角形组成的图形．
练习册系列答案
相关题目