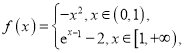题目内容
【题目】函数![]() 的图象的对称轴之间的最短距离为
的图象的对称轴之间的最短距离为![]() ,且经过点
,且经过点![]() .
.
(1)写出函数![]() 的解析式;
的解析式;
(2)若对任意的![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)求实数![]() 和正整数
和正整数![]() ,使得
,使得![]() 在
在![]() 上恰有2017个零点.
上恰有2017个零点.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 时,
时,![]() ;
;![]() 时,
时,![]()
【解析】
(1)由对称轴及图像上一点,待定系数可得函数解析式;
(2)求![]() 值域,换元后,转化为二次函数恒成立问题求参数;
值域,换元后,转化为二次函数恒成立问题求参数;
(3)将零点问题转化为交点问题,先考虑一个周期的情况,再进行延拓.
(1)![]() 的图象的对称轴之间的最短距离为
的图象的对称轴之间的最短距离为![]() ,
,
故其周期为![]() ,解得
,解得![]() ;
;
又![]() 经过点
经过点![]() ,故
,故![]() ,
,
解得![]()
又因为![]() ,故可得
,故可得![]() ,
,
故![]() .
.
(2)若对任意的![]() ,
,![]() ,
,
故![]() ,
,
因为![]() 恒成立,
恒成立,
令![]() ,
,
![]() 恒成立,只需:
恒成立,只需:
![]() ,且
,且![]() ,
,
解得![]() .
.
(3)∵![]() 在
在![]() 上恰有2017个零点,
上恰有2017个零点,
故![]() 的图象和直线
的图象和直线![]() 在
在![]() 上恰有2017个交点.
上恰有2017个交点.
先考虑在在![]() 上的交点情况,
上的交点情况,
不妨作出![]() 在
在![]() 上的图像如下:
上的图像如下:
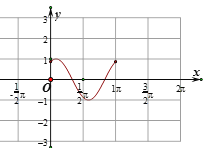
①当![]() ,或
,或![]() 时,
时,
![]() 的图象和直线
的图象和直线![]() 在
在![]() 上无交点.
上无交点.
②当![]() ,或
,或![]() 时,
时,
![]() 的图象和直线
的图象和直线![]() 在
在![]() 仅有一个交点,
仅有一个交点,
此时,![]() 的图象和直线
的图象和直线![]() 在
在![]() 上恰有2017个交点,
上恰有2017个交点,
则![]() .
.
③当![]() ,或
,或![]() 时,
时,
![]() 的图象和直线
的图象和直线![]() 在
在![]() 上恰有2个交点,
上恰有2个交点,
![]() 的图象和直线
的图象和直线![]() 在
在![]() 上有偶数个交点,不会有2017个交点.
上有偶数个交点,不会有2017个交点.
④当![]() 时,
时,
![]() 的图象和直线
的图象和直线![]() 在
在![]() 上恰有3个交点,
上恰有3个交点,
此时,![]() ,才能使
,才能使![]() 的图象和直线
的图象和直线![]() 在
在![]() 上有2017个交点.
上有2017个交点.
综上可得,当![]() ,或
,或![]() 时,
时,![]() ;
;
当![]() 时,此时,
时,此时,![]() .
.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目