Question

设x、y满足1≤x+y≤4和y+2≥|2x-3|,

(1)求点(x,y)所表示的平面区域;

(2)设a＞-1,在(1)所确定的区域里,求函数f(x,y)=y-ax的最大值和最小值.

Answer 1

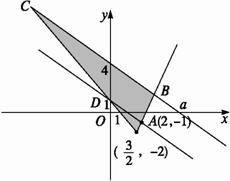
解析：(1)点(x,y)所在的平面区域如图(阴影部分).?

其中AB:y=2x-5,CD:y=-2x+1,AD:x+y=1,BC:x+y=4.?

(2)f(x,y)是直线l:y-ax=k在y轴上的截距,直线l必与阴影相交.由a＞-1,则l通过顶点C时,f(x,y)最大.又C点的坐标为(-3,7),于是f(x,y)的最大值为3a+7.?

如果-1＜a≤2,则l通过点A(2,-1)时,f(x,y)最小,此时最小值为-2a-1.?

如果a＞2,则l通过点B(3,1)时,f(x,y)最小,此时最小值为-3a+1.