题目内容
如图,在平面斜坐标系xoy中,∠xoy=60°,平面上任一点P在斜坐标系中的斜坐标是这样定义的:若 =xe1+ye2(其中e1、e2分别为与x轴、y轴方向相同的单位向量),则P点的斜坐标为(x,y).若P点的斜坐标为(3,-4),则点P到原点O的距离|PO|= .
=xe1+ye2(其中e1、e2分别为与x轴、y轴方向相同的单位向量),则P点的斜坐标为(x,y).若P点的斜坐标为(3,-4),则点P到原点O的距离|PO|= .
【答案】分析:在理解P点的斜坐标的基础上,根据p点的坐标表示出向量  ,进而由|
,进而由| |2=(3e1-4e2)2可得答案.
|2=(3e1-4e2)2可得答案.
解答:解:∵P点斜坐标为(3,-4),
∴ =3e1-4e2.
=3e1-4e2.
∴| |2=(3e1-4e2)2=25-24e1•e2=25-24×cos60°=13.
|2=(3e1-4e2)2=25-24e1•e2=25-24×cos60°=13.
∴| |=
|= ,即|OP|=
,即|OP|= .
.
故答案为: .
.
点评:本题主要考查平面向量的坐标表示和运算,解答的关键是对新定义的斜坐标的理解.
 ,进而由|
,进而由| |2=(3e1-4e2)2可得答案.
|2=(3e1-4e2)2可得答案.解答:解:∵P点斜坐标为(3,-4),
∴
 =3e1-4e2.
=3e1-4e2.∴|
 |2=(3e1-4e2)2=25-24e1•e2=25-24×cos60°=13.
|2=(3e1-4e2)2=25-24e1•e2=25-24×cos60°=13.∴|
 |=
|= ,即|OP|=
,即|OP|= .
.故答案为:
 .
.点评:本题主要考查平面向量的坐标表示和运算,解答的关键是对新定义的斜坐标的理解.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图,在平面斜坐标系xoy中,∠xoy=60°,平面上任一点P关于斜坐标系的斜坐标这样定义的,若
如图,在平面斜坐标系xoy中,∠xoy=60°,平面上任一点P关于斜坐标系的斜坐标这样定义的,若| OP |
| A、x2+y2=1 |
| B、x2+y2+xy=1 |
| C、x2+y2-xy=1 |
| D、x2+y2+2xy=1 |
 如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的:
如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的: 如图,在平面斜坐标系XOY中,∠xoy=θ,平面上任意一点P关于斜坐标系的斜坐标这样定义:若
如图,在平面斜坐标系XOY中,∠xoy=θ,平面上任意一点P关于斜坐标系的斜坐标这样定义:若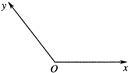 如图,在平面斜坐标系xOy中,∠xOy=135°.斜坐标定义:如果
如图,在平面斜坐标系xOy中,∠xOy=135°.斜坐标定义:如果 (2008•宝山区一模)如图,在平面斜坐标系中xoy中,∠xoy=60°,平面上任一点P的斜坐标定义如下:若
(2008•宝山区一模)如图,在平面斜坐标系中xoy中,∠xoy=60°,平面上任一点P的斜坐标定义如下:若