题目内容
设P是边长为a的正△ABC内的一点,P点到三边的距离分别为h1、h2、h3,则 ;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4= .
;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4= .
【答案】分析:由平面图形的性质向空间物体的性质进行类比时,常用的思路有:由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质,由平面图形中面的性质类比推理出空间中体的性质.固我们可以根据已知中平面几何中,关于线的性质“正三角形内任意一点到三边距离之和是一个定值”,推断出一个空间几何中一个关于面的性质.
解答: 解:类比P是边长为a的正△ABC内的一点,
解:类比P是边长为a的正△ABC内的一点,
本题可以用一个正四面体来计算一下棱长为a的三棱锥内任一点到各个面的距离之和,
如图:
由棱长为a可以得到BF= a,BO=AO=
a,BO=AO= ,
,
在直角三角形中,根据勾股定理可以得到
BO2=BE2+OE2,
把数据代入得到OE= a,
a,
∴棱长为a的三棱锥内任一点到各个面的距离之和4× a=
a= a,
a,
故答案为: a.
a.
点评:本题考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).
解答:
 解:类比P是边长为a的正△ABC内的一点,
解:类比P是边长为a的正△ABC内的一点,本题可以用一个正四面体来计算一下棱长为a的三棱锥内任一点到各个面的距离之和,
如图:
由棱长为a可以得到BF=
 a,BO=AO=
a,BO=AO= ,
,在直角三角形中,根据勾股定理可以得到
BO2=BE2+OE2,
把数据代入得到OE=
 a,
a,∴棱长为a的三棱锥内任一点到各个面的距离之和4×
 a=
a= a,
a,故答案为:
 a.
a.点评:本题考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

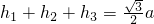 ;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4=________.
;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4=________. ;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4= .
;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4= .