题目内容
(1)求(1+2x)7的展开式中的第3项的系数.
(2)求(|x|+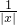 -2)3展开式中的常数项.
-2)3展开式中的常数项.
解:(1)(1+2x)7展开式的通项为Tr+1= ,则(1+2x)7的展开式中的第3项的系数为
,则(1+2x)7的展开式中的第3项的系数为 ×22=84;
×22=84;
(2)(|x|+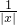 -2)3=
-2)3=
设第r+1项为常数项,则Tr+1=C6r•(-1)r•( )6-r•(
)6-r•( )r=(-1)6•C6r•(
)r=(-1)6•C6r•( )6-2r,
)6-2r,
∴6-2r=0,∴r=3.
∴T3+1=(-1)3•C63=-20.
分析:(1)写出展开式的通项,令r=2,即可求得结论;
(2)(|x|+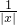 -2)3=
-2)3= ,写出通项,令x的指数为0,即可求得展开式中的常数项.
,写出通项,令x的指数为0,即可求得展开式中的常数项.
点评:本题考查解决二项展开式的特定项问题,考查二项展开式的通项公式,属于中档题.
 ,则(1+2x)7的展开式中的第3项的系数为
,则(1+2x)7的展开式中的第3项的系数为 ×22=84;
×22=84;(2)(|x|+
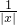 -2)3=
-2)3=
设第r+1项为常数项,则Tr+1=C6r•(-1)r•(
 )6-r•(
)6-r•( )r=(-1)6•C6r•(
)r=(-1)6•C6r•( )6-2r,
)6-2r,∴6-2r=0,∴r=3.
∴T3+1=(-1)3•C63=-20.
分析:(1)写出展开式的通项,令r=2,即可求得结论;
(2)(|x|+
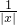 -2)3=
-2)3= ,写出通项,令x的指数为0,即可求得展开式中的常数项.
,写出通项,令x的指数为0,即可求得展开式中的常数项.点评:本题考查解决二项展开式的特定项问题,考查二项展开式的通项公式,属于中档题.

练习册系列答案
相关题目