题目内容
(1)求(1+2x)7展开式中系数最大项;
(2)求(1-2x)7展开式中系数最大项.
(2)求(1-2x)7展开式中系数最大项.
(1)设第r+1项系数最大,则有
,
即
,
即
,
∴
≤r≤
且0≤r≤7,r∈Z,
∴r=5.
∴系数最大项为T6=C75•25•x5=672x5;
(2)展开式共有8项,系数最大项必为正项,
即在第一、三、五、七这四项中取得,
故系数最大项必在中间或偏右,
∴只需比较T5和T7两项系数大小即可.
∵T5=C74(-2)4x4=560x4,T7=C76(-2)6x6=448x6,
∴系数最大的项是第五项为T5=C74(-2)4x4=560x4.
|
即
|
即
|
∴
| 13 |
| 3 |
| 16 |
| 3 |
∴r=5.
∴系数最大项为T6=C75•25•x5=672x5;
(2)展开式共有8项,系数最大项必为正项,
即在第一、三、五、七这四项中取得,
故系数最大项必在中间或偏右,
∴只需比较T5和T7两项系数大小即可.
∵T5=C74(-2)4x4=560x4,T7=C76(-2)6x6=448x6,
∴系数最大的项是第五项为T5=C74(-2)4x4=560x4.

练习册系列答案
相关题目
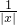 -2)3展开式中的常数项.
-2)3展开式中的常数项.